nextnano³ - Tutorial

next generation 3D nano device simulator

3D Tutorial

Strain effects in freestanding three-dimensional nitride nanostructures

Author: Stefan Birner, M. Povolotskyi

If you want to obtain the input files that are used within this tutorial, please check if you can find them in the installation directory.
If you cannot find them, please submit a Support Ticket.
-> 3DGaNAlGaN_QW_strain_freestanding_nn3.in - input file for the nextnano³ software
-> 3DGaNAlGaN_QW_strain_freestanding_nnp.in - input file for the nextnano++ software
 

Strain effects in freestanding three-dimensional nitride nanostructures

-> 3DGaNAlGaN_QW_strain_freestanding_nn3.in

In this tutorial, we study the strain in lattice mismatched three-dimensional freestanding heterostructures of wurtzite crystal structure.
The calculated strain pattern of this AlGaN/GaN nanowire is found to be highly nonhomogeneous.
The elastic energy has been minimized using continuum elasticity theory.
We assume that the external stress applied to the structure is zero (freestanding structure).

This tutorial is based on the following paper:

[Povolotskyi]
Strain effects in freestanding three-dimensional nitride nanostructures
M. Povolotskyi, M. Auf der Maur, A. Di Carlo
physica status solidi (c) 2, 3891 (2005)

The following figure shows the AlGaN / GaN / AlGaN quantum well structure.
A 4 nm wide GaN QW layer is embedded between two Al_0.28Ga_0.72N layers.
The bottom AlGaN layer has a width of 10 nm, the top AlGaN layer has a width of 6 nm.

The overall shape of this nitride nanowire structure has the form of a cuboid with 50 nm x 50 nm extensions in the x and y directions.
The height in the z direction is 20 nm.
The overall structure is surrounded by air (i.e. with a material where all elastic constants are zero).
 

The material interfaces are perpendicular to the hexagonal c axis of the wurtzite lattice, i.e. perpendicular to the [0001] crystallographic direction. The QW is grown along the [0001] direction (z direction).

  $domain-coordinates
   ...
   hkil-x-direction =  1  0 -1  0 ! x axis of simulation coordinate system
 ! hkil-y-direction = -1  2 -1  0 ! y axis of simulation coordinate system
   hkil-z-direction =  0  0  0  1 ! z axis of simulation coordinate system

Freestanding structure

  $simulation-flow-control
   ...
   strain-calculation = strain-minimization-new  ! strain routine necessary for freestanding structure
 

  $strain-minimization-model           ! for strain-calculation = strain-minimization
   ...
   grown-on-substrate       = no       ! freestanding structure
 ! grown-on-substrate       = yes      ! thick substrate (default) - not used in this tutorial!
 

Results

Strain tensor components of the freestanding nitride heterostructure

The following figures show the strain tensor components e_ij(x,y,z) as a function of coordinates (x,y,z) of slices through the structure where x = constant (vertical cross section of the structure).

The slices are perpendicular to the x direction [1 0 -1 0] and are positioned in the center of the structure.

Note that GaN has a larger lattice constant than AlGaN.
Consequently, we expect the GaN layer to be compressively strained and the AlGaN layers to be tensilely strained (or rather unstrained).

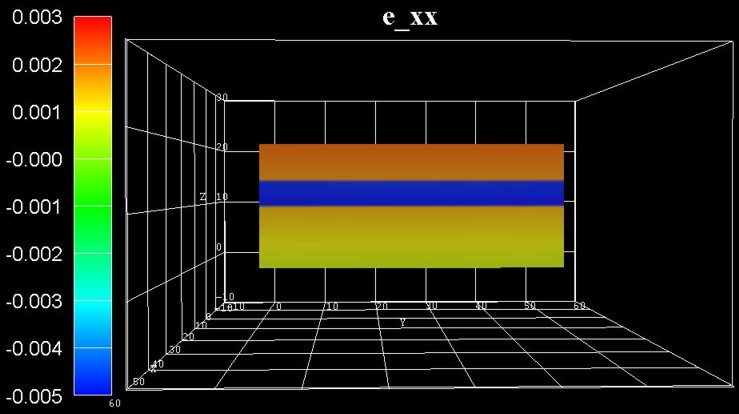
The following figure shows the strain tensor component e_xx.

==> strain1/e_sim_xx3D.fld / *.coord / *.dat

The bottom AlGaN layer is rather unstrained (at the bottom), the GaN QW layer is strained compressively along the x direction (blue region).
This is not a surprise as we assumed coherent interfaces, i.e. the atomic planes match each other perfectly (pseudomorphic strain).
The GaN QW induces a tensile strain to the AlGaN top layer (red region).

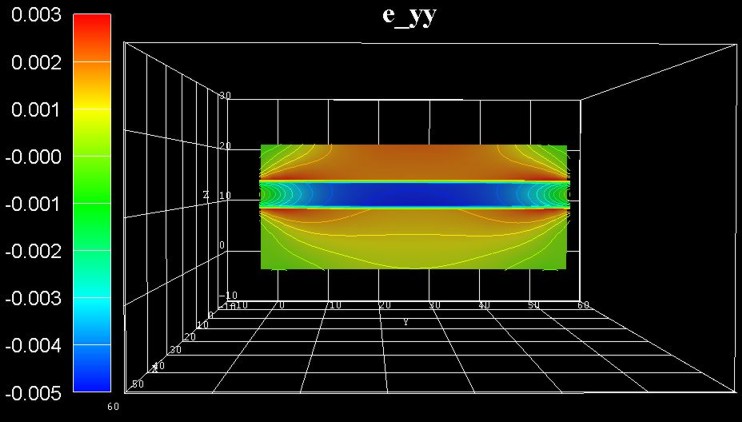
The following figure shows the strain tensor component e_yy.
Similar to the figure for the e_xx component, the GaN layer is compressively strained (blue region) but only in the center and not at the boundaries where it is nearly relaxed.
Note that the e_xx and e_yy strain tensor components are not symmetric. This is due to the nitride crystal structure which has hexagonal symmetry perpendicular to the (x,y) plane (and not cubic symmetry as the geometry of the structure).
- In the center (blue region), the GaN takes on the lattice constant of AlGaN (compressive strain).
- At the QW boundaries, the GaN takes on the lattice constant of ~GaN (nearly fully relaxed).
- Below and above the QW boundaries (red regions), the AlGaN takes on the lattice constant of ~GaN (tensile strain).

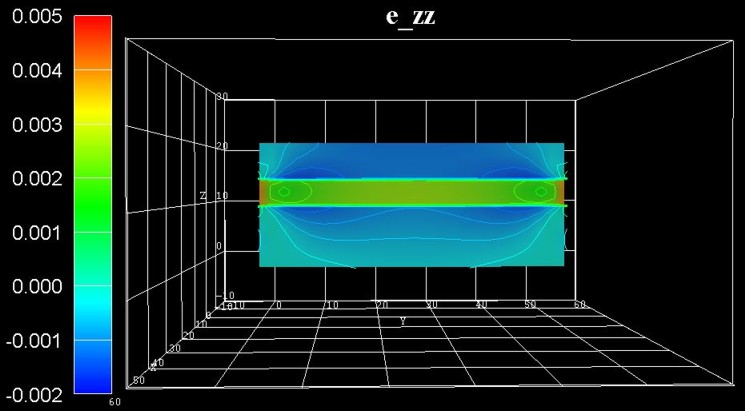
The following figure shows the strain tensor component e_zz.
As the GaN layer is compressively strained along both the x and y directions,
it is tensilely strained (green region) along the z direction (biaxially strained GaN layer, Poisson ratio).

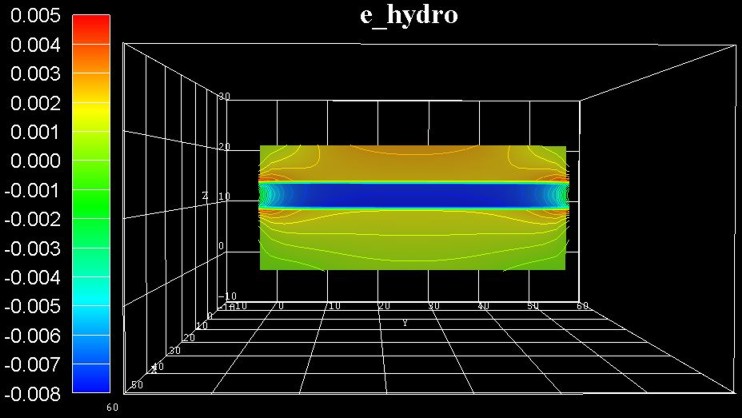
The following figure shows the hydrostatic strain e_hydro = e_xx + e_yy + e_zz  which is the trace of the strain tensor, i.e. the sum of the diagonal strain tensor components. It corresponds to the overall volume change.

==> strain1/e_hydro3D.fld / *.coord / *.dat

The blue region indicates that the GaN is strained compressively.
AlGaN is mostly unstrained apart from the red regions at the left and right boundaries of the material interfaces.

In a real sample, due to the deformation, the heterostructure changes its shape and becomes bended.
In our case, the strain is small (less than 1%), so the shape of the structure does not change significantly.

In contrast to heterostructures which are infinitely large and homogeneous in the lateral directions (i.e. in the (x,y) plane), the deformation of a structure of a finite size is not homogeneous, as e.g. in GaN nanowire heterostructures.

Since the structure is grown along the high symmetry direction [0001], the strain patterns exhibits reflection symmetry along the axis through the center (oriented parallel to the z axis).
The deformation becomes homogeneous in the region near the central axis, reproducing the case of an infinitely large structure.

The following figure shows the offdiagonal strain tensor component e_yz.

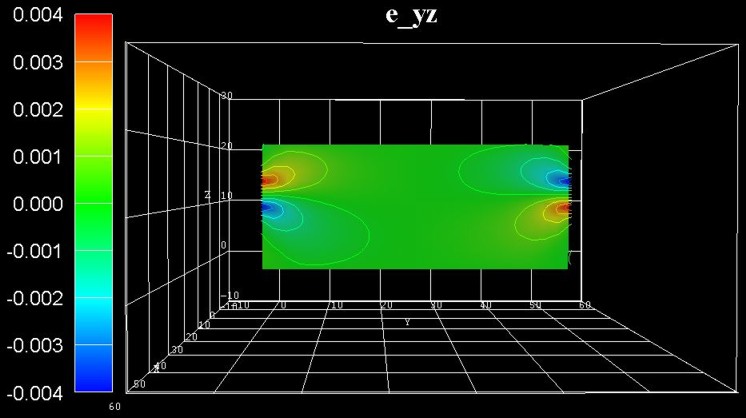
The strain tensor components e_xy and e_xz are zero for this particular slice.
(In fact, the maximum value of e_xy is an order of magnitude smaller that the maximum value of e_xz or e_yz.)

The following figure shows the same offdiagonal strain tensor component e_yz but this time at slices at the left and right boundaries.

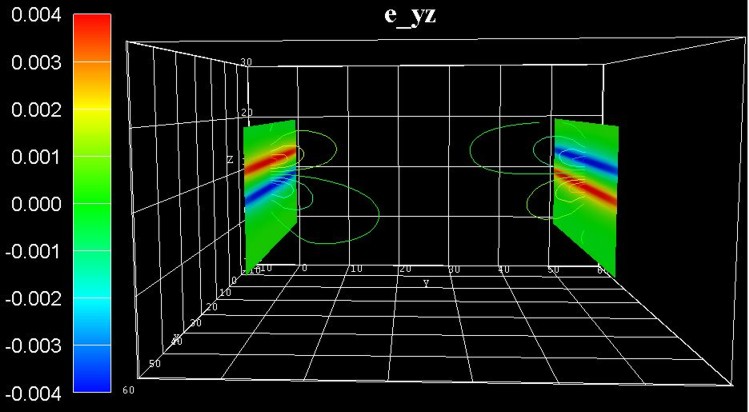
Due to a possible usage of such structures as a light emitter, the strain in the GaN layer where charge carriers are confined, is or particular interest, i.e. the influence of stain on the conduction and valence band structure through deformation potentials.
Additionaly, piezoelectric and pyroelectric fields have to be taken into account.
The piezoelectric fields depend on the strain distribution in the sample.
Thus both the piezoelectric field and the GaN energy gap will vary along the lateral direction.

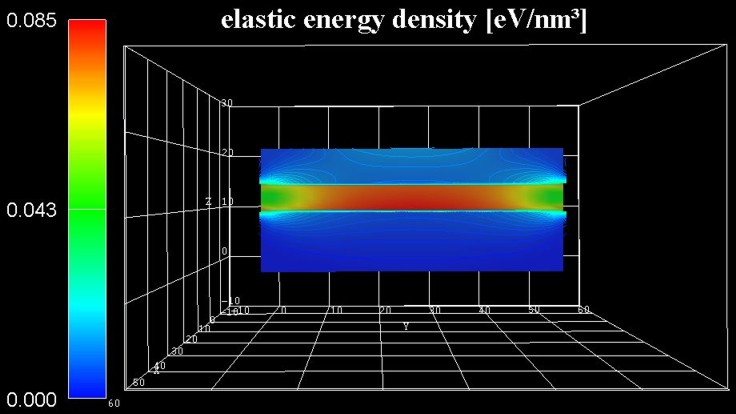
This figure shows the energy density of the elastic deformation in units of [eV/nm3].
The accumulated elastic energy in the pseudomorphically grown GaN QW is gradually reduced towards the free surface along the lateral direction.
Consequently, the GaN QW center is almost fully strained, whereas towards the lateral surface there is a continous relaxation.

==> strain1/ElasticEnergyDensity3D_eV.fld / *.coord / *.dat

These figures are part of the output, i.e. 2D slices of the 3D data. This can be done as follows:

!---------------------------------------------------------------------------!
$output-section !
section-number = 1   section-name = slice_middle_along               section-type = z   x = 25.0 y = 25.0 ! 1D slice through center along z axis
section-number = 2   section-name = slice_middle_parallel_QW_plane   section-type = xy  z = 12.0          ! 2D slice in the middle of QW, parallel to the QW plane
section-number = 3   section-name = slice_middle_perp_QW_plane       section-type = yz  x = 25.0          ! 2D slice in the middle perpendicular to the QW plane
section-number = 4   section-name = slice_boundary_perp_QW_plane     section-type = xz  y = 2.0           ! 2D slice at the boundary perpendicular to the QW plane
$end_output-section !
!---------------------------------------------------------------------------!
 

Similar figures can also be found in these papers:

• Columnar AlGaN/GaN Nanocavities with AlN/GaN Bragg Reflectors Grown by Molecular Beam Epitaxy on Si(111)
  J. Ristić, E. Calleja, A. Trampert, S. Fernández-Garrido, C. Rivera, U. Jahn, K. H. Ploog
  Phys. Rev. Lett. 94, 146102 (2005)
• Carrier-confinement effects in nanocolumnar GaN∕AlxGa1−xN quantum disks grown by molecular-beam epitaxy
  J. Ristić, C. Rivera, E. Calleja, S. Fernández-Garrido, M. Povoloskyi, A. Di Carlo
  Phys. Rev. B 72, 085330 (2005)
• Strain-confinement mechanism in mesoscopic quantum disks based on piezoelectric materials
  C. Rivera, U. Jahn, T. Flissikowski, J. L. Pau, E. Muñoz, and H. T. Grahn
  Phys. Rev. B 75, 045316 (2007)