nextnano³ - Tutorial

next generation 3D nano device simulator

1D Tutorial

k.p dispersion in bulk GaAs (strained / unstrained)

Note: This tutorial's copyright is owned by Stefan Birner, www.nextnano.de.

Author: Stefan Birner

If you want to obtain the input files that are used within this tutorial, please contact stefan.birner@nextnano.de.
-> 1Dbulk_kp_dispersion_GaAs.in
-> 1Dbulk_kp_dispersion_GaAs_3D.in
-> 1Dbulk_kp_dispersion_GaAs_strained.in

Band structure of bulk GaAs

• We want to calculate the dispersion E(k) from |k|=0 to |k|=0.1 along the following directions in k space:
  - [000] to [001]
  - [000] to [011]
  We compare 6x6 and 8x8 k.p theory results.
• We calculate E(k) for bulk GaAs at a temperature of 300 K.

Step 1: Bulk dispersion along [001]

• $output-kp-data
 destination-directory = kp_data1/

 bulk-kp-dispersion    = yes
 grid-position         = 5d0              ! in units of [nm]
 !----------------------------------------
 ! Dispersion along [001] direction
 ! maximum |k| vector = 0.10 [1/Angstrom]
 !----------------------------------------
 k-direction           = 0d0  0d0  0.10d0 ! k-direction and range for dispersion plot [1/Angstrom]

 number-of-k-points    = 100 ! number of k points to be calculated (resolution)
   shift-holes-to-zero   = yes ! 'yes' or 'no'
$end_output-kp-data
• We calculate the pure bulk dispersion at grid-position=5d0, i.e. for the material located at the grid point at 5 nm. In our case this is GaAs but it could be any strained alloy. In the latter case, the k.p Bir-Pikus strain Hamiltonian will be diagonalized.
  The grid point at grid-position must be located inside a quantum cluster.
  shift-holes-to-zero = yes forces the top of the valence band to be located at 0 eV.
  How often the bulk k.p Hamiltonian should be solved can be specified via number-of-k-points. To increase the resolution, just increase this number.
• Start the calculation.
  The results of step 1 can be found in kp_data1/bulk_8x8kp_dispersion000_kxkykz.dat.

Step 2: Bulk dispersion along [011]

• $output-kp-data
 destination-directory = kp_data1/

 bulk-kp-dispersion    = yes
 grid-position         = 5d0              ! in units of [nm]
 !----------------------------------------
 ! Dispersion along [011] direction
 ! maximum |k| vector = 0.10 [1/Angstrom]
 !----------------------------------------
 k-direction           = 0d0  0.07071d0  0.07071d0 ! k-direction and range for dispersion plot [1/Angstrom]

 number-of-k-points    = 100 ! number of k points to be calculated (resolution)
   shift-holes-to-zero   = yes ! 'yes' or 'no'
$end_output-kp-data
• Here we use another direction, i.e. from [000] to [011]. The maximum value of |k| is SQRT(0.07071² + 0.07071²) = 0.1.
  Note that for values of |k| larger than 0.1, k.p theory might not be a good approximation any more.
• Start the calculation.
  The results of step 2 can be found in kp_data1/bulk_8x8kp_dispersion000_kxkykz.dat.

Step 3: Plotting E(k)

• Here we will have to visualize the results of both Step 1 and Step 2.
• The final figure will look like this:
  
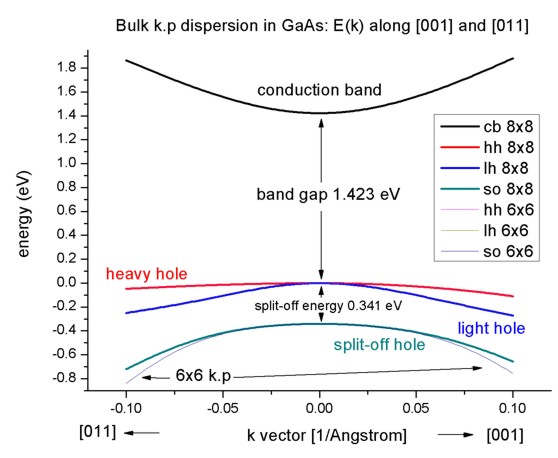
  The split-off energy of 0.341 eV is identical to the split-off energy as defined in the database:
    6x6-kp-parameters = ... 0.341d0
 
• If one zooms into the holes and compares 6x6 vs. 8x8 k.p, one can see that 6x6 and 8x8 coincide for |k| < 0.1 for the heavy and light hole but differ for the split-off hole at larger |k| values.
  
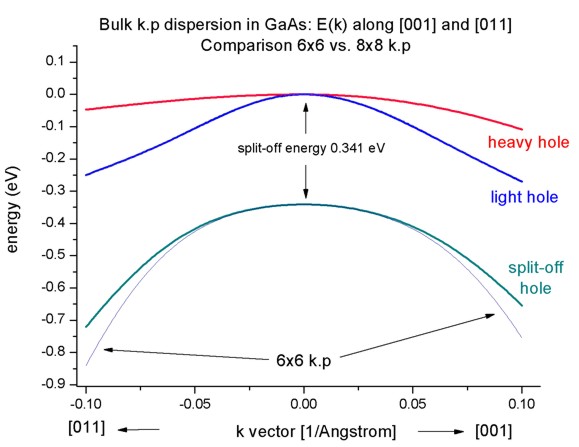
  To switch between 6x6 and 8x8 k.p one only has to change this entry in the input file:
  $quantum-model-holes
 ...
 model-name = 8x8kp ! for 8x8 k.p
            = 6x6kp ! for 6x6 k.p

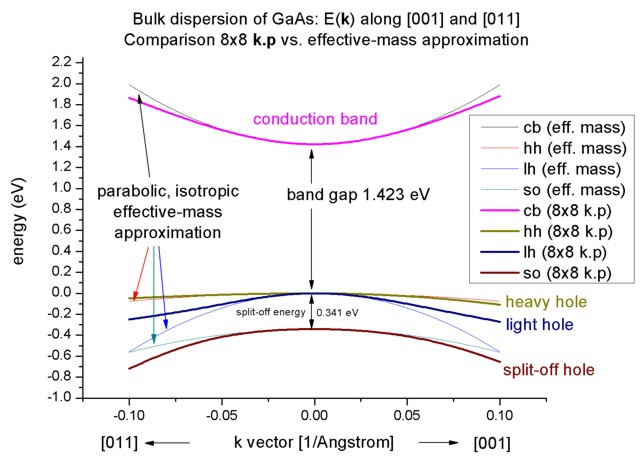
8x8 k.p vs. effective-mass approximation

• Now we want to compare the 8x8 k.p dispersion with the effective-mass approximation. The effective mass approximation is a simple parabolic dispersion which is isotropic (i.e. no dependence on the k vector direction). For low values of k (|k| < 0.4) it is in good agreement with k.p theory.
  The output data can be find here:
  kp_data1/bulk_sg_dispersion000_kxkykz.dat.
  
  

Band structure of strained GaAs

• Now we perform these calculations again for GaAs that is strained with respect to In_0.2Ga_0.8As. The InGaAs lattice constant is larger than the GaAs one, thus GaAs is strained tensilely.
• The changes that we have to make in the input file are the following:
  
  $simulation-flow-control
 ...
 strain-calculation  = homogeneous-strain
$end_simulation-flow-control

$domain-coordinates
 ...
 pseudomorphic-on    = In(x)Ga(1-x)As
 alloy-concentration = 0.20d0
$end_domain-coordinates

As substrate material we take In_0.2Ga_0.8As and assume that GaAs is strained pseudomorphically (homogeneous-strain) with respect to this substrate, i.e. GaAs is subject to a biaxial strain.
• Due to the positive hydrostatic strain (i.e. increase in volume or negative hydrostatic pressure) we obtain a reduced band gap with respect to the unstrained GaAs.
  Furthermore, the degeneracy of the heavy and light hole at k=0 is lifted.
  Now, the anisotropy of the holes along the different directions [001] and [011] is very pronounced. There is even a band anti-crossing along [001]. (Actually, the anti-crossing looks like a "crossing" of the bands but if one zooms into it (not shown in this tutorial), one can easily see it.)
  Note: If biaxial strain is present, the directions along x, y or z are not equivalent any more. This means that the dispersion is also different in these directions ([100], [010], [001]).
  
  
  
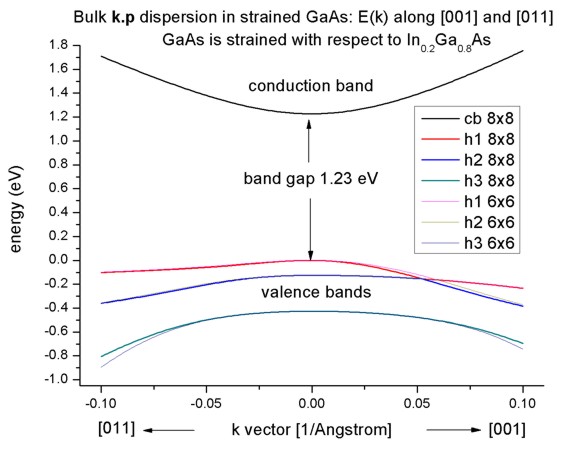
• If one zooms into the holes and compares 6x6 vs. 8x8 k.p, one can see that the agreement between heavy and light holes is not as good as in the unstrained case where 6x6 and 8x8 k.p lead to almost identical dispersions.
  
  
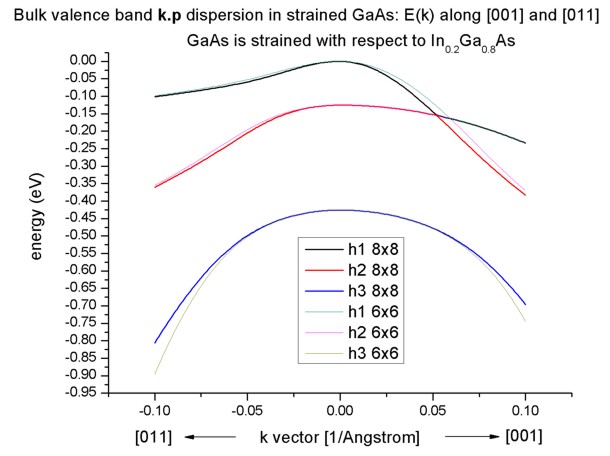
  Note that in the strained case, the effective-mass approximation is very poor.

• Please help us to improve our tutorial! Send comments to support [at] nextnano.de.