nextnano³ - Tutorial

next generation 3D nano device simulator

1D Tutorial

GaN/AlN wurtzite structure: Strain, piezo and pyroelectric charges in wurtzite

Author: Stefan Birner

-> 1Dwurtzite_nn3_noStrain_noPiezo_noPyro_noPoisson.in             - input file for the nextnano³ software
-> 1Dwurtzite_nn3.in                                   / *_nnp.in  - input file for the nextnano³ and nextnano++ software
-> 1Dwurtzite_nn3_Nface.in                             / *_nnp.in  - input file for the nextnano³ and nextnano++ software

These input files are included in the latest version.

GaN/AlN structure

• This input file simulates a GaN/AlN/GaN wurtzite structure: 1Dwurtzite.in
  The structure is grown pseudomorphically on GaN, i.e. the AlN is tensilely strained, the GaN is unstrained. The growth direction [0001] is along z, the interfaces are in the (x,y) plane. As we have [0001] growth direction, we have Ga-polar GaN (i.e. Ga-face polarity).
• No strain.
  $numeric-control
 simulation-dimension            = 1
 zero-potential                  = yes
 varshni-parameters-on           = no  ! Band gaps independent of temperature. Absolute values from database are taken.
   lattice-constants-temp-coeff-on = no  ! Lattice constants independent of temperature. Absolute values from database are taken.
   piezo-constants-zero            = yes ! Piezoelectric constants are set to zero.
   pyro-constants-zero             = yes ! Pyroelectric  constants are set to zero.
  $end_numeric-control
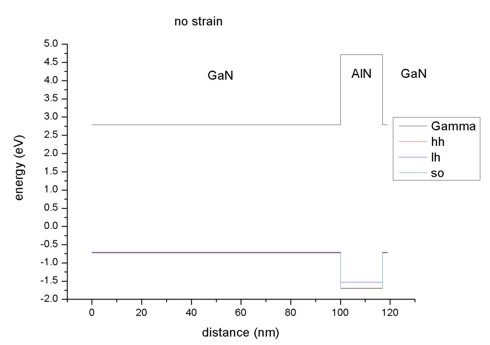
• The pictures shows the conduction and valence band edges of the heterostructure when no strain is applied (strain-calculation = no-strain). AlN is the barrier for both electrons and holes.
  
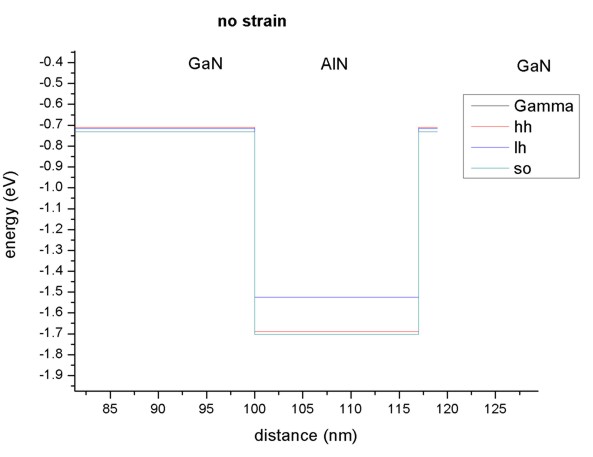
  Now we zoom into the valence band structure. In AlN the light hole lies above the heavy hole, in GaN the situation is the opposite. Note that heavy and light hole are not degenerate (as would be the case in zinc blende).
  
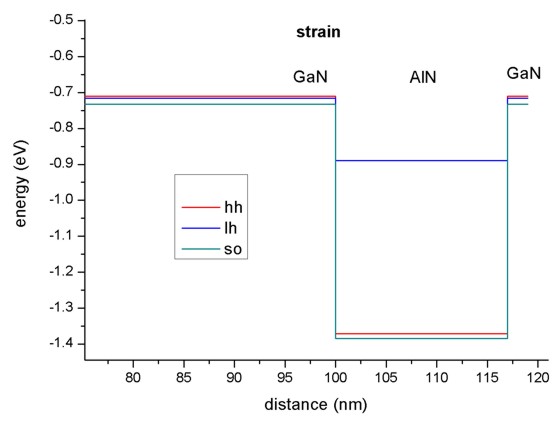
• Pseudomorphic strain.
  strain-calculation = homogeneous-strain
pseudomorphic-on   = GaN ! lattice constant a=0.3189 nm (lattice constant c does not matter for this growth direction)
The GaN is unstrained, the AlN (lattice constant a=0.3112 nm; elastic constants c₁₃=108.0, c₃₃=373.0) is tensilely strained as it has the smaller lattice constant.
  The biaxial strain is tensile: eps_|| = (a_substrate - a) / a = 0.0247429
  The uniaxial strain is compressive: eps_{_|_}= - 2 c₁₃/c₃₃ eps_|| = - 0.0143283
  The hydrostatic strain is positive which corresponds to an increase in volume for AlN: eps_hy = Tr(eps_ij) = (2 eps_|| + eps_{_|_}) = 0.0351575
  The strain leads to a shift in the conduction and valence band edges.
  
  Conduction band at Gamma:
  In wurtzite the crystal anisotropy leads to two distinct conduction band deformation potentials for the Gamma point, one is parallel and the other one is perpendicular to the c axis.
   absolute-deformation-potentials-cbs = a_{c,a axis}     a_{c,a axis}      a_{c,c axis}
   absolute-deformation-potentials-cbs =  -3.9d0  -3.9d0 -20.5d0 ! [eV]
Thus the conduction band edge energy including the hydrostatic energy shift is given by:
E_c′ = E_c + a_{c,c axis} eps_{_|_} + 2a_{c,a axis} eps_|| = 4.712 + (-20.5 * (-0.0143283) ) + 2 (-3.9) * 0.0247429 = 4.712 + 0.10073553 = 4.81274 eV
  So in this particular example, the barrier for electrons is increased.
  
   uniax-cb-deformation-potentials-cbs = 0d0  0d0  0d0
Data for uniaxial deformation potentials of other minima than Gamma are not available yet. At the Gamma point, the uniaxial deformation potential is zero.
  
  Valence bands:
  From a full treatment of the effect of strain on the six-band Hamiltonian six valence band deformation potentials arise.
   uniax-vb-deformation-potentials     =    d1    d2    d3    d4    d5    d6  ! [eV]
 uniax-vb-deformation-potentials     = -17.1   7.9   8.8  -3.9  -3.4  -3.4  ! [eV]
In contrast to zinc blende, an absolute deformation potential for the valence band is not needed.
   absolute-deformation-potential-vb   = 0d0 ! (Not needed, should be removed from wurtzite database in the future.)
  The shifts of the valence bands are obtained by diagonalizing the Bir-Pikus strain Hamiltonian which is given in Basics 2 (strain effects). This is a general approach as it gives the correct shifts for arbitrary orientations (However, it is only for valence bands).
  In our example, the tensile strain in AlN shifts all holes upwards,
  - the heavy hole by 0.31687 eV,
  - the light hole by 0.63565 eV and
  - the crystal field split-off hole by 0.31717 eV,
  thus reducing the barrier for the holes.
  
• Pyroelectric polarization (spontaneous polarization)
  $numeric-control
 pyro-constants-zero = no
  The wurtzite materials GaN, AlN and InN are pyroelectric materials and thus show a spontaneous polarization.
  Thy pyroelectric field P^py is along the hexagonal z direction (along c axis) and it is always negative. P^py is directed from anion to cation. The positive z direction (i.e. [0001]) is from cation to anion.
  GaN: P^py = - 0.034 C/m²
  AlN:  P^py = - 0.090 C/m²
  At the interfaces we have a discontinuity of P^py(z). The pyroelectric polarizations at the interfaces are determined as follows:
  1^st  interface at 100 nm (GaN/AlN): P^py(left point) - P^py(right point) = - 0.034 + 0.090 =   0.056 C/m²
  2^nd interface at 117 nm (AlN/GaN): P^py(left point) - P^py(right point) = - 0.090 + 0.034 = - 0.056 C/m²
  The interface charges can be found in the output file interface_densitiesD.txt ($output-densities).
  The interface charge of -0.056 C/m² corresponds to 34.952*10¹² electrons /cm².
  Once having determined the pyroelectric polarization P^py one is able to compute the pyroelectric charge density: rho_py(x) = - div P^py(x).
  If the hexagonal axis is oriented along the z axis as in our example, this equation reduces to: rho_py(z) = - d/dz P^py(z)
  The pyroelectric charge density per cm³ is given in density1Dpyro.dat.
  In pyro_polarization.dat the pyroelectric constant as given in the database or input file is plotted for each grid point.
• Piezoelectric polarization
  $numeric-control
 piezo-constants-zero = no
  If AlN is strained, piezoelectric fields arise.
  In GaN the piezoelectric polarization is zero as there is no strain.
  AlN: e₃₃ = 1.79, e₃₁ = - 0.50 (e₁₅ is not relevant for [0001] growth direction)
  In AlN the piezoelectric polarization is:
  P^pz = e₃₃eps_{_|_} + e₃₁ (eps_|| + eps_||) = 1.79 * (- 0.0143283) - 0.50 * 2 * 0.0247429 = - 0.050390 C/m²
  P^pz is directed in this example parallel to P^py as the piezoelectric polarization is negative for tensilely strained AlN grown on GaN.
  GaN: P^pz = 0 C/m²  (no strain)
  AlN:  P^pz = - 0.050390 C/m²
  At the interfaces we have a discontinuity of P^pz(z). The piezoelectric polarizations at the interfaces are determined as follows:
  1^st  interface at 100 nm (GaN/AlN): P^pz(left point) - P^pz(right point) = 0 + 0.050390   =    0.050390 C/m²
  2^nd interface at 117 nm (AlN/GaN): P^pz(left point) - P^pz(right point) = - 0.050390 - 0 = - 0.050390 C/m²
  The interface charges can be found in the output file interface_densitiesD.txt ($output-densities).
  The interface charge of -0.050390 C/m² corresponds to 31.451*10¹² electrons /cm².
  Once having determined the piezoelectric polarization P^pz one is able to compute the piezoelectric charge density: rho_pz(x) = - div P^pz(x).
  The piezoelectric charge density per cm³ is given in density1Dpiezo.dat.
  In our 1D example, this equation reduces to: rho_pz(z) = - d/dz P^pz(z)
  In piezo_polarization.dat the piezoelectric constants (e₃₃, e₃₁, e₁₅) as given in the database or input file are plotted for each grid point.
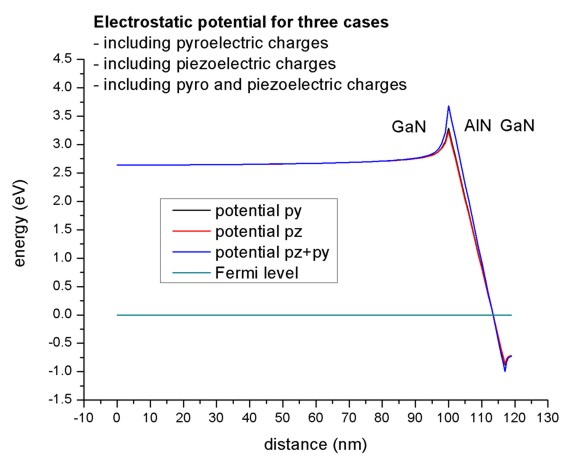
• Electrostatic potential including piezo and pyroelectric charges.
  The electrostatic potential is the solution of the nonlinear Poisson equation.
  - div (ε(r) grad phi(r)) = rho(r,phi)
  The charge density rho contains the (static) piezo and pyroelectric charge densities as well as the electron and hole charge densities and ionized donors and acceptors. The latter depend on the electrostatic potential phi but the piezo and pyroelectric charge densities don't.
  (zero-potential = no)
  Here we plot the electrostatic potential in units of eV for three different cases:
  - including pyroelectric  charges         (piezo-constants-zero = no , pyro-constants-zero = yes)
  - including piezoelectric charges        (piezo-constants-zero = yes, pyro-constants-zero = no)
  - including pyro and piezoelectric charges (piezo-constants-zero = no , pyro-constants-zero = no)
  In our example the piezo and pyroelectric contributions are of the same size. The Fermi level is set to zero.
  
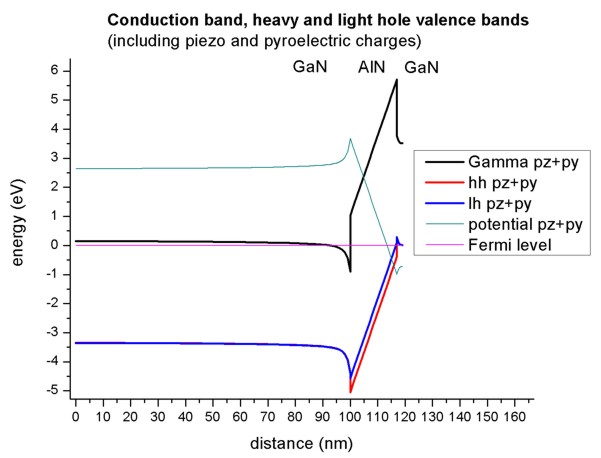
• The electrostatic potential in units of eV has to be substracted from the conduction and valence band edges. The resulting band structure is plotted in this figure (The piezo and pyroelectric charges were considered in this calculation).
  Note that the conduction band is pulled below the Fermi level (around 98 nm) and the valence band above the Fermi level (around 118 nm).
  

N-face polarity

This input file simulates a GaN/AlN/GaN wurtzite structure (N-face polarity): 1Dwurtzite_Nface.in
The structure is the same as above. The only difference is the polarity: N-face instead of Ga-face.

The above examples correspond to Ga-face polarity. In order to investigate N-face polarity, we have to switch from [0001] growth direction to [000-1] growth direction (z -> -z). In order to keep a right-handed coordinate axes system we also invert the x direction (x -> -x). The third direction (here: the y direction) is calculated automatically (internally).

 $domain-coordinates
  domain-type            = 0 0 1
  z-coordinates          = 0.0d0 119d0
  growth-coordinate-axis = 0 0 1          ! along z direction
  pseudomorphic-on       = GaN

  !********************************
  ! This is along [0001] direction: Ga-face polarity

  ! hkil-x-direction =  1 0 -1 0          ! Miller-Bravais indices of x coordinate axis [ 1 0 -1 0]
  !!hkil-y-direction = -1 2 -1 0          ! Miller-Bravais indices of y coordinate axis [-1 2 -1 0]
  ! hkil-z-direction =  0 0  0 1          ! Miller-Bravais indices of z coordinate axis [ 0 0 0 -1]

  ! Equivalent Bravais indices
  ! hkl-x-direction-zb = 1 0 0            ! Miller indices of x coordinate axis [1 0 0]
  ! hkl-y-direction-zb = 0 1 0            ! Miller indices of y coordinate axis [0 1 0]
  ! hkl-z-direction-zb = 0 0 1            ! Miller indices of z coordinate axis [0 0 1]
  !********************************

  !********************************
  ! This is along [000-1] direction: N-face polarity

    hkil-x-direction = -1 0  1  0 ! => -x ! Miller-Bravais indices of x coordinate axis [-1 0  1  0]
  ! hkil-y-direction = -1 2 -1  0         ! Miller-Bravais indices of y coordinate axis [-1 2 -1  0]
    hkil-z-direction =  0 0  0 -1 ! => -z ! Miller-Bravais indices of z coordinate axis [ 0 0  0 -1]

  ! Equivalent Bravais indices
  ! hkl-x-direction-zb = -1  0  0         ! Miller indices of x coordinate axis [1 0 0]
  ! hkl-y-direction-zb =  0  1  0         ! Miller indices of y coordinate axis [0 1 0]
  ! hkl-z-direction-zb =  0  0 -1         ! Miller indices of z coordinate axis [0 0 1]
  !********************************
 

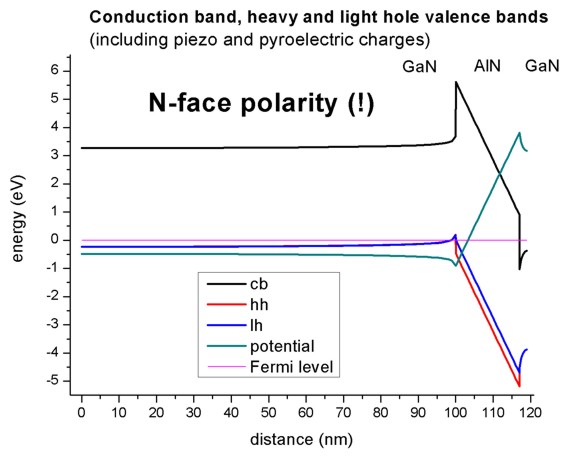
The figure shows the Fermi level (at 0 eV), the electrostatic potential and the conduction and valence band edges (heavy and light hole) of the N-face heterostructure.
(The piezo and pyroelectric charges were considered in this calculation).
Note the difference in comparison to the figure above for the Ga-face case. The location of the 2DEGs and 2DHGs (two-dimension hole gases) is reversed.

An alternative way of switching from Ga-face to N-face would have been to change the sign of the pyroelectric constants.

The boundary conditions for the Poisson equation in this simulation were Neumann boundary conditions, i.e. the derivative of the electrostatic potential is zero at the boundaries (flat band boundary conditions).
No doping was present in this simulation.

Note: The figures shown in this tutorial have been generated a long time ago. The actual results may differ from these figures because the input files now contain a modified grid space resolution, and modified layer widths, as well as a different total structure size.