nextnano.com
 nextnano³
 Download | Search | Copyright | Publications
 * password protected

 

nextnano³ software

 

  2D DG MOSFET

 

 

 
Up
 

nextnano3 - Tutorial

next generation 3D nano device simulator

2D Tutorial

Ultrathin-body Double Gate FET - DG MOSFET (Double Gate Metal Oxide Semiconductor Field Effect Transistor)

Author: Stefan Birner

-> 2DDoubleGateMOSFET_nn3_05grid.in  / *nnp*.in - input file for the nextnano3 and nextnano++ software (2D simulation)
-> 3DDoubleGateMOSFET_nn3_05grid.in             - input file for the nextnano3 software (3D simulation)

These input files are included in the latest version.

DG MOSFET (Double Gate Metal Oxide Semiconductor Field Effect Transistor)

The main idea of a Double Gate MOSFET is to control the Si channel very efficiently by choosing the Si channel width to be very small and by applying a gate contact to both sides of the channel. This concept helps to suppress short channel effects and leads to higher currents as compared with a MOSFET having only one gate.

 

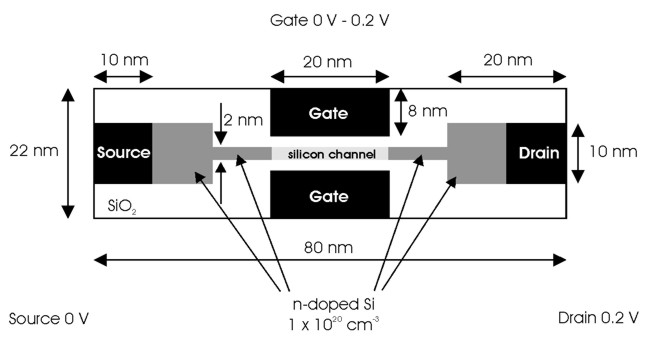
  • Double Gate MOSFET (Metal Oxide Semiconductor Field Effect Transistor)
                (grown on Si substrate, i.e. unstrained)

    The Double Gate MOSFET contains the following regions
     

    cluster

    region

    		  

    color

    		  
    1 1 Source and drain are connected with the Si channel blue
    2 2 Source (metal) left
    3 3 Drain (metal) right
    4 4  5 Gate / Backgate (metal) top/bottom
    5 6  7 Doped source and drain region (Si) blue
    6 8 The insulating material is SiO2. red (default region)

    Both the regions 4 (gate) and 5 (backgate) form the cluster no. 4.

    The width of the Si channel is 2 nm.
    The distance between the two gates is 6 nm, i.e. the isolating SiO2 is 2 nm thick on each side. The width of the two gates is 20 nm.

    The distance between source and drain is 60 nm. The widths and the lengths of source, drain, left and right doped source regions are 10 nm x 10 nm each. The length of the 2 nm Si channel (without the square doped source and drain regions) is 40 nm.
     

          
       Top gate     (Schottky barrier 3.445 V)
    0 V ... 0.2 V

    		  

    Source (0.0 V)

    		Drain  (0.2 V)
     

                  Bottom gate (Schottky barrier 3.445 V)
    0 V ... 0.2 V

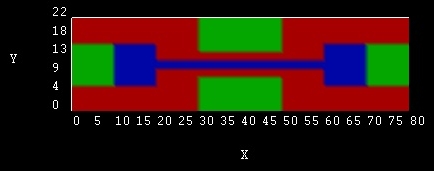
    Schematic top view of the Double Gate MOSFET

    		  

    The blue squares (Si) are n-doped with a a concentration of 1x1020 cm-3.
    The 2 nm channel is n-doped with the same concentration from 20 to 30 and from 50 to 60 nm.

     $doping-function

      doping-function-number = 1                     !     Source
      impurity-number        = 1
      doping-concentration   = 1d2                   ! 1 x 1020 cm-3
      only-region            = 0d0 20d0    6d0 16d0  ! xmin xmax ymin ymax

      doping-function-number = 2                     !     Si channel (left)
      impurity-number        = 1
      doping-concentration   = 1d2                   ! 1 x 1020 cm-3
      only-region            = 20d0 30d0   10d0 12d0 ! xmin xmax ymin ymax

      doping-function-number = 3                     !     Si channel (right)
      impurity-number        = 1
      doping-concentration   = 1d2                   ! 1 x 1020 cm-3
      only-region            = 50d0 60d0   10d0 12d0 ! xmin xmax ymin ymax

      doping-function-number = 4                     !     Drain
      impurity-number        = 1
      doping-concentration   = 1d2                   ! 1 x 1020 cm-3
      only-region            = 60d0 80d0   6d0 16d0  ! xmin xmax ymin ymax

     $end_doping-function

     $impurity-parameters
      impurity-number             = 1
      impurity-type               = n-type
      number-of-energy-levels     = 1
      energy-levels-relative      = 0.044d0  !     energy relative to 'nearest' conduction band edge in units of [eV]
      degeneracy-of-energy-levels = 2        !     degeneracy of energy levels, 2 for n-type
     $end_impurity-parameters
     
  • At the two gates we apply a Schottky barrier of 3.443 eV:
     $poisson-boundary-conditions
      ...
      poisson-cluster-number  = 3         !     top and bottom gate
      region-cluster-number   = 4
      applied-voltage         = 0d0
      boundary-condition-type = schottky
      schottky-barrier        = 3.443d0
      contact-control         = voltage
      ...
     $end_poisson-boundary-conditions

    The source and drain contacts are ohmic.
    - Source: 0.0 V
    - Drain:    0.2 V

    A voltage sweep varies the gate (top gate and bottom gate) voltage from 0 to 2.0 V in 10 steps.
     $voltage-sweep
      sweep-number            = 1
      sweep-active            = yes
      poisson-cluster-number  = 3    !     Gate: poisson-cluster-number = 3
      step-size               = 0.1d0
      number-of-steps         = 10
      data-out-every-nth-step = 1
     $end_voltage-sweep
     
  • Gridding
     

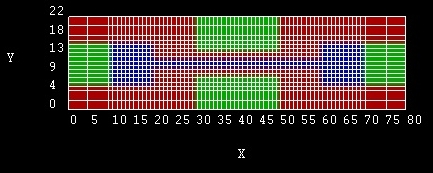    Grid lines of the Double Gate MOSFET

    Note: The grid lines that are shown in the figure are the material grid lines. The grid lines that one specifies in the input file are the physical grid lines. The material grid lines are placed half-way between the physical grid lines. For more information on the definition of the grid confer this page: Grids and Geometry

 

How to run the input file...

  • The lattice temperature is taken to be 300 Kelvin.
    The flow scheme is 4 for a classical self-consistent calculation:
       - calculate nonlinear Poisson classically
       - calculate current classically
    No strain will be considered here.
  • This time we perform a two-dimensional simulation. The overall simulation domain, that is the real space region in which the device is defined, is taken to be a rectangle having the size 22 nm x 80 nm.
  • Just a reminder: If you need additional information about the keywords and their specifiers, you can look them up here.
  • Output
    - The band structure (conduction and valence bands) will be saved into the directory band_structure/.
    - The densities (electron densities) will be saved into densities/.
    - Current data (Fermi levels, current density and I-V characteristics) will be saved into current/.
    - The raw data for the potentials and the Fermi levels (can be read in later in subsequent runs) will be saved into raw_data/.

    Output files that will be produced are:

  • The output files can be read in with the AVS/Express software that can be obtained by Advanced Visual Systems.
    AVS output files     described in the next three paragraphs:
    - material_grid.fld
    - material_grid.coord
    - material_grid.dat
  • - material_grid.fld
    This is an AVS field file specifiying the input files and data format needed for processing the 2D/3D visualisation.

     # AVS field file         !
     #                        !
     ndim   =  2              !     dimension of data
     dim2   = 18              !     no. of grid points in y direction
     dim1   = 66              !     no. of grid points in x direction
     nspace =  2              !     dimension of data
     veclen =  1              !     length of data vector (1 means scalar quantity)
     data   = float           !     data type - integer/float
     field  = rectilinear     !     rectilinear coordinate system
     label  = material_grid2D !     name of data files to be proceeded

     variable 1 file=material_grid2D.dat   filetype=ascii skip=0 offset=  0 stride=1

     coord 2    file=material_grid2D.coord filetype=ascii skip=0 offset=  0 stride=1
     coord 1    file=material_grid2D.coord filetype=ascii skip=0 offset= 18 stride=1

    These three lines specify where the data is located in each file:
    The y coordinates are located at position 0 to 18 in the file material_grid.coord, x coordinates are located in the same file at position 19 to 84.
    The variable data is stored in the .dat file and is related to the coordinates in a systematic order.
  • AVS input files: material_grid.coord, material_grid.dat
  • - material_grid.coord
        Coordinates of the grid, i.e. 18+66 real numbers that specify the grid points on each axis.
  • - material_grid.dat
        Contains information about the regions.
        Each grid point is specified by a region number as defined in the input file (see table at top of this page).
  • All other folders contain the same structure for AVS field files:
    - *.fld
    - *.coord
    - *.dat
  • Now we try to plot some nice pictures of our Double Gate MOSFET...

    1) Electron density at 0 V Gate voltage:
    densities/density2Del_ind000.*
     


    Electron density at 0 V Gate voltage (Drain voltage 0.2 V)

    The Si region is n-doped with 1 x 1020 cm-3 from x=10 to 30 nm and from x=50 to 70 nm. The units of the electron density are 1 x 1018 cm-3.


    2) Electron density at 0.2 V Gate voltage:
    densities/density2Del_ind010.dat
     


    Electron density at 0.2 V Gate voltage (Drain voltage 0.2 V)

    The Si region is n-doped with 1 x 1020 cm-3 from x=10 to 30 nm and from x=50 to 70 nm. The units of the electron density are 1 x 1018 cm-3.
    One can clearly see that the electron density has the highest values at the Si-SiO2 interfaces.



    Quantum mechanical electron density at 0.2 V Gate voltage (Drain voltage 0.2 V)

    The Si region is n-doped with 1 x 1020 cm-3 from x=10 to 30 nm and from x=50 to 70 nm. The units of the electron density are 1 x 1018 cm-3.
    One can clearly see that the electron density has the highest values in the middle of the channel and not at the Si-SiO2 interfaces. This is because the wave functions tend to zero at the Si-SiO2 interfaces.
    The peak values in the source and drain regions are due to classical densities because the quantum region did not extend over the whole source and drain regions.

 

Results

  • The current-voltage (I-V) characteristic can be found in the following file: current/IV_characteristics2D.dat
    The drain voltage is kept constant at 0.2 V, the gate voltage varies from 0 to 2.0 V.
    The figure shows the I-V characteristics for three different mobility models, compared with the results obtained with a commercial software package. The units for the current in a 2D simulation are [A/m] (but can be adjusted to [A/cm]).

    - mobility-model-simba-0 (no dependence on electric field)
    - mobility-model-simba-2 (mobility depends on parallel electric field)
      In this case the current is smaller because the mobility decreases when the applied voltage increases.
    - mobility-model-lom (Lombardi mobility model)

    More information on the mobility models can be found here:
    - $mobility-model-simba     (SIMBA mobility model)
    - $mobility-model-lom (Lombardi mobility model)



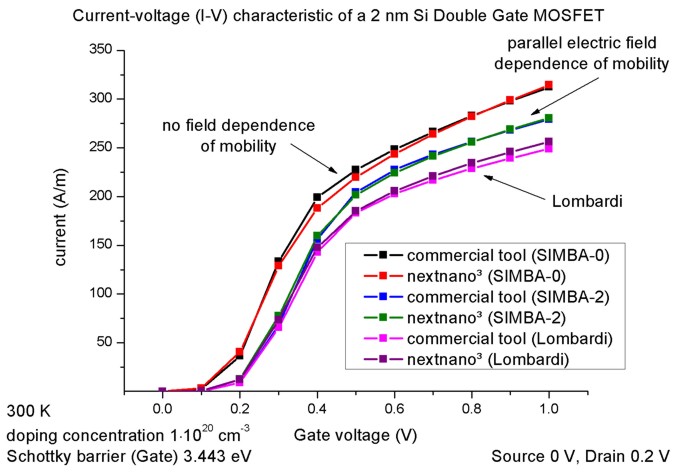
    Note    : This is a classical calculation. So no quantum mechanical effects are included. For a quantum mechanical calculation, the current is smaller. This is mainly due to the difference in the classical and quantum mechanical electron density.
     

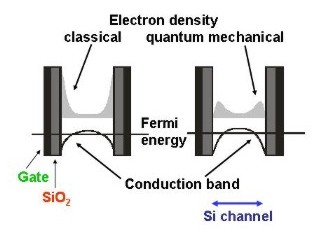
    Classical and quantum mechanical electron density as seen when cutting through the Si channel.
    (Note: In this figure, the Si channel is larger than 2 nm.)

    In the classical simulation, the electron density has its maximum at the SiO2-Si interface.
    In the quantum mechanical simulation, however, the electron density is basically zero at the SiO2-Si interface.

 

3D

 -> 3DDoubleGateMOSFET_nn3_05grid.in

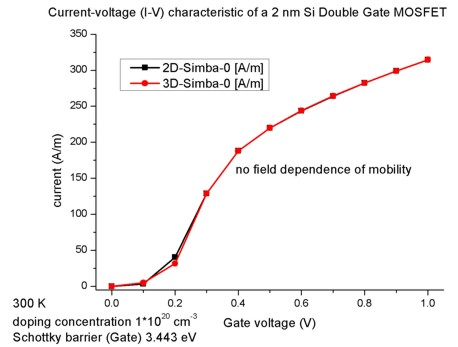
In order to test the nextnano³ implementation of the three-dimensional drift-diffusion current, we calculated this Double Gate MOSFET in a three-dimensional simulation. We assume that the structure is homogeneous along the z direction and assume the z direction to be 10 nm long (grid spacing 2 nm). The units of the current are in [A] (current/IV_characteristics3D.dat). The current has to be divided by the length of the device along the z direction, i.e. by 10 nm, in order to obtain it in units of [A/m]. The 3D results are in agreement with the 2D results.

Comparison of the 2D and 3D nextnano³ results for mobility-model-simba-0.