nextnano³ - Tutorial

next generation 3D nano device simulator

1D Tutorial

Quantum-Cascade Laser

Author: Stefan Birner

If you want to obtain the input files that are used within this tutorial, please check if you can find them in the installation directory.
If you cannot find them, please submit a Support Ticket.
 

-> 1DQuantumCascadeLaser.in -> 1DQCL_AlGaAs_Sirtori_APL73_1998.in -> 1DQCL_Andrea_Friedrich_NoInjector_InGaAs_APL86_2005_77K_kp.in -> 1DQCL_Andrea_Friedrich_NoInjector_InGaAs_APL86_2005_300K_kp.in -> 1DQCL_Rochat_APL81_2002.in -> 1DQCL_THz_MIT_Sandia_SemicScTech20_2005.in -> THzQCL_Andrews_Vienna_MatSciEng2008_nn3.in / *_nnp.in - input file for nextnano³ and nextnano++ software -> 1DQuantumCascadeLaserSiGe_nn3.in           / *_nnp.in - input file for nextnano³ and nextnano++ software

Quantum-Cascade Laser

This tutorial is based on the quantum-cascade structure that has been presented in the following paper.

300 K operation of a GaAs-based quantum-cascade laser at lambda=9 µm
H. Page, C. Becker, A. Robertson, G. Glastre, V. Ortiz, C. Sirtori
Applied Physics Letters 78 (22), 3529 (2001)

Here, we are trying to reproduce Fig. 1 of this paper.

The temperature has been set to 300 K.

The quantum-cascade structure consists of a sequence of GaAs wells and Al_0.45Ga_0.55As barriers. The sequence is as follows (from 0 nm to 45 nm; it is repeated outside this region):

4.6 / 1.9 / 1.1 / 5.4 / 1.1 / 4.8 / 2.8 / 3.4 / 1.7 / 3.0 / 1.8 / 2.8 / 2.0 / 3.0 / 2.6 / 3.0

The units are [nm]. Blue and bold scripts indicate Al_0.45Ga_0.55As barriers, normal scripts indicate GaAs wells.

In the APL paper, a conduction band offset of 390 meV was used.
Consequently, we modify our default band offset by shiftting the AlGaAs ternary slightly to also get 390 meV.

 $ternary-zb-default
  ternary-type = Al(x)Ga(1-x)As-zb-default
  ...
  band-shift   = 0.022719d0                 ! [eV] ==> to get a band offset of 390 meV for T=300 K and x=0.45 (Al_0.45Ga_0.55As)
 

We apply an electric field of -48 kV/cm:

 $electric-field                    !
  electric-field-on        = yes    ! 'yes' / 'no'
  electric-field-strength  = -48d5  ! in units of [V/m] - Here: -48 kV/cm
  electric-field-direction = 0 0 1  ! [001] direction, i.e. along z axis.
 $end_electric-field                !
 

For simplicity, in contrast to the APL paper, we do not include doping here.
In the original APL paper, the following areas were n-type doped with silicon with a sheet density of n_Si = 3.8 * 10¹¹ cm^-2.
=> between 15.2 nm and -5.6 nm (9.8 nm): '1.8 nm' (barrier), '2.8 nm' (well), '2.0 nm' (barrier) and '3.0 nm' (well)
=> between 29.8 nm and 39.4 nm (9.8 nm): '1.8 nm' (barrier), '2.8 nm' (well), '2.0 nm' (barrier) and '3.0 nm' (well)

We use flow-scheme = 21.

 $simulation-flow-control
! flow-scheme = 20   ! ==> apply electric field and        solve Poisson equation
  flow-scheme = 21   ! ==> apply electric field and do not solve Poisson equation
  ...

These flow-schemes includes the following:
1. Calculate the strain (if any).
2. Calculate the piezo and pyroelectric charges (if any).
3. Calculate the conduction and valence band edge profiles by solving Poisson's equation taking into acount doping (if any), piezo and pyroelectric charges (if any) and deformation potentials (if strain unequal to zero).
4. Apply the electric field.
5. Calculate the eigenstates and wave functions by solving Schrödinger's equation (either single-band or k.p).
Note that for flow-scheme = 21, this is not a self-consistent calculation of the Poisson-Schrödinger equation.
flow-scheme = 20 is self-consistent but a severe limitation is that population inversion is not taken into account.

In our example, we did not have to calculate the strain. Piezo any pyroelectric fields do not exist. We do not include doping. We used single-band (effective-mass) rather than 8-band k.p.

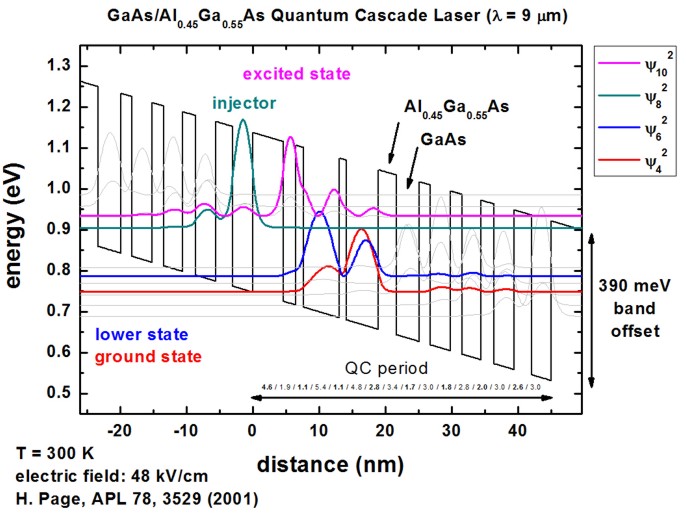
The following figure shows the conduction band energy of the Gamma conduction band edge and the wave functions (psi² = psi squared) of the ground state 1, the lower state 2, the excited state 3 and the injector state i.

The above shown structure of the conduction band edge and the wave functions is in excellent agreement with Fig. 1 of the following paper:

300 K operation of a GaAs-based quantum-cascade laser at lambda=9 µm
H. Page, C. Becker, A. Robertson, G. Glastre, V. Ortiz, C. Sirtori
Applied Physics Letters 78 (22), 3529 (2001)

Note that periodic boundary conditions for the Schrödinger and Poisson equation do not make sense because of the application of an electric field. Thus we used Dirichlet boundary conditions. However, this will lead to some artificial, wrong wave functions at the boundaries because the wave function is forced to be zero at the boundaries. For the states in the middle of the device where the wave function decays to zero in any case at the boundaries, the boundary conditions do not have any influence at all and so these states are fine.
So the suggestion is to calculate 3 or 5 periods, and then take the energy levels and wave functions of the center period.
In this way, boundary effects should not be very severe.

 $quantum-model-electrons
   model-number           = 1
   model-name             = effective-mass  ! 'effective-mass' or '8x8kp'
   boundary-condition-001 = Dirichlet       ! boundary condition for [001] direction, i.e. along the z direction
   ...

Intraband matrix elements

QCL examples

Note: We have nextnano³ input files available for quantum-cascade lasers that are based on the following structures.
Please submit a support ticket if you want to obtain these input files.

• 9 µm, i.e. 33 THz or 138 meV
  300 K operation of a GaAs-based quantum-cascade laser at lambda=9 µm
  H. Page, C. Becker, A. Robertson, G. Glastre, V. Ortiz, C. Sirtori
  Applied Physics Letters 78 (22), 3529 (2001)
  
  -> 1DQuantumCascadeLaser.in
 
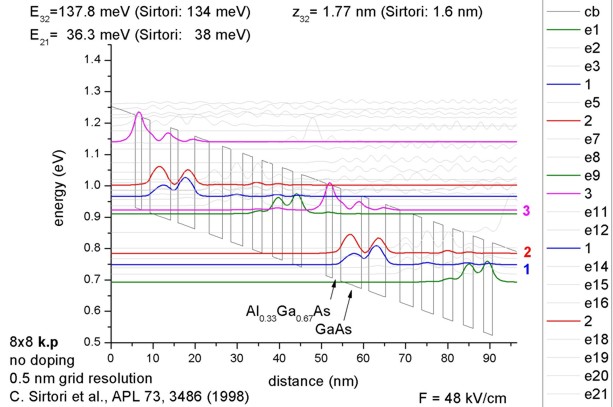
• 9.4 µm or 132 meV
  GaAs/Al_xGa_1-xAs quantum cascade lasers
  C. Sirtori, P. Kruck, S. Barbieri, P. Collot, J. Nagle, M. Beck, J. Faist, U. Oesterle
  Applied Physics Letters 73 (24), 3486 (1998)
  
  -> 1DQCL_AlGaAs_Sirtori_APL73_1998.in

  
   
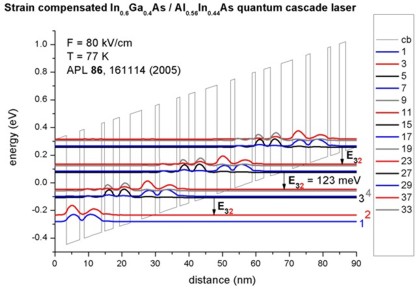
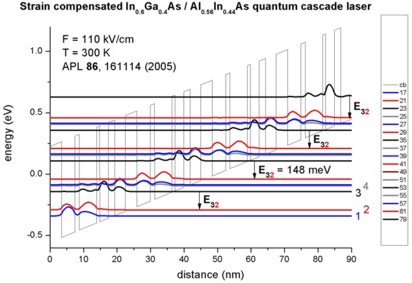
• 10 µm, i.e. 124 meV (77 K)
  8.4 µm, i.e. 148 meV (300 K)
  Quantum-cascade lasers without injector regions operating above room temperature
  A. Friedrich, G. Böhm, M.C. Amann, G. Scarpa
  Applied Physics Letters 86, 161114 (2005)
  
  -> 1DQCL_Andrea_Friedrich_NoInjector_InGaAs_APL86_2005_77K_kp.in
-> 1DQCL_Andrea_Friedrich_NoInjector_InGaAs_APL86_2005_300K_kp.in


 
• 66 µm, i.e. 4.54 THz or 18.8 meV (nextnano³ calculation: 18.5 meV, i.e. 4.47 THz or 67 µm)
  Low-threshold terahertz quantum-cascade lasers
  M. Rochat, L. Ajili, H. Willenberg, J. Faist, H. Beere, G. Davies, E. Linfield, D. Ritchie
  Applied Physics Letters 81 (8), 1381 (2002)
  
  -> 1DQCL_Rochat_APL81_2002.in

  Note: The caption in FIG. 1 in this paper must read "from right to left", rather than "from left to right".
  
  
   
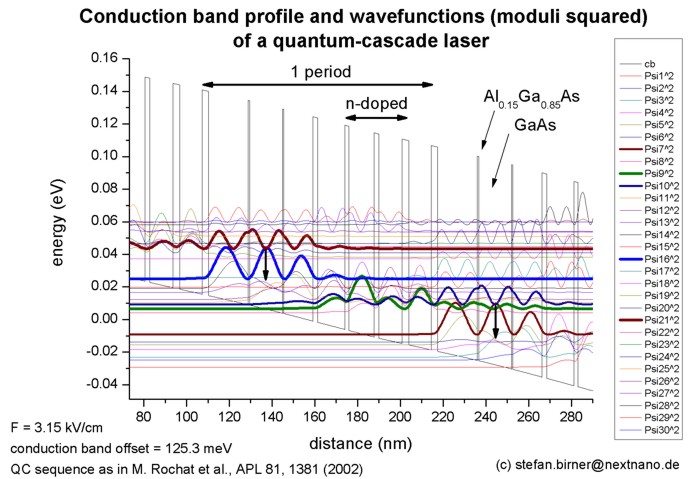
• 89.2 µm, i.e.  3.4 THz or 13.9 meV (exp. 14.2 meV) (nextnano³ calculation: 14.02 meV)
  Resonant-phonon-assisted THz quantum-cascade lasers with metal-metal waveguides
  Q. Hu, B.S. Williams, S. Kumar, H. Callebaut, S. Kohen, J.L. Reno
  Semiconductor Science and Technology 20, S228 (2005)
  
  -> 1DQCL_THz_MIT_Sandia_SemicScTech20_2005.in

  
   
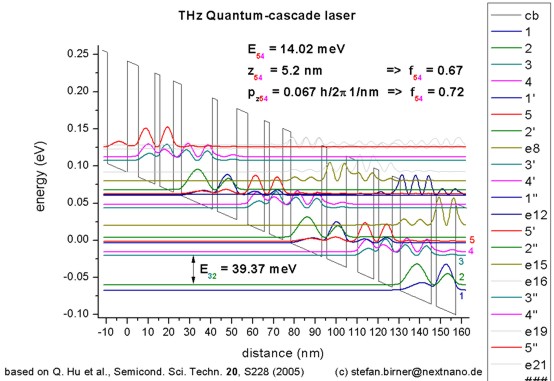
• 107 µm, i.e. 2.8 THz or 11 meV
  
  Doping dependence of LO-phonon depletion scheme THz quantum-cascade lasers
  A. M. Andrews, A. Benz, C. Deutsch, G. Fasching, K. Unterrainer, P. Klang, W. Schrenk, G. Strasser
  Materials Science and Engineering B 147, 152 (2008)
  
  -> THzQCL_Andrews_Vienna_MatSciEng2008_nn3.in - input file for nextnano³ software
-> THzQCL_Andrews_Vienna_MatSciEng2008_nnp.in - input file for nextnano++ software
  
  
  
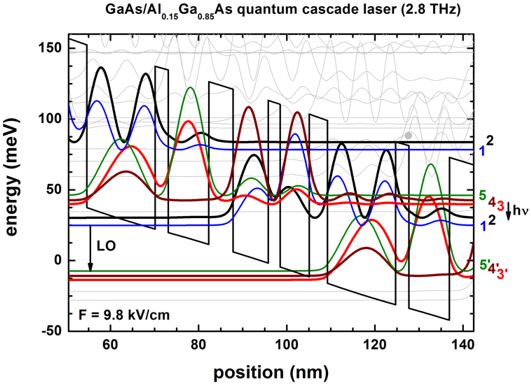
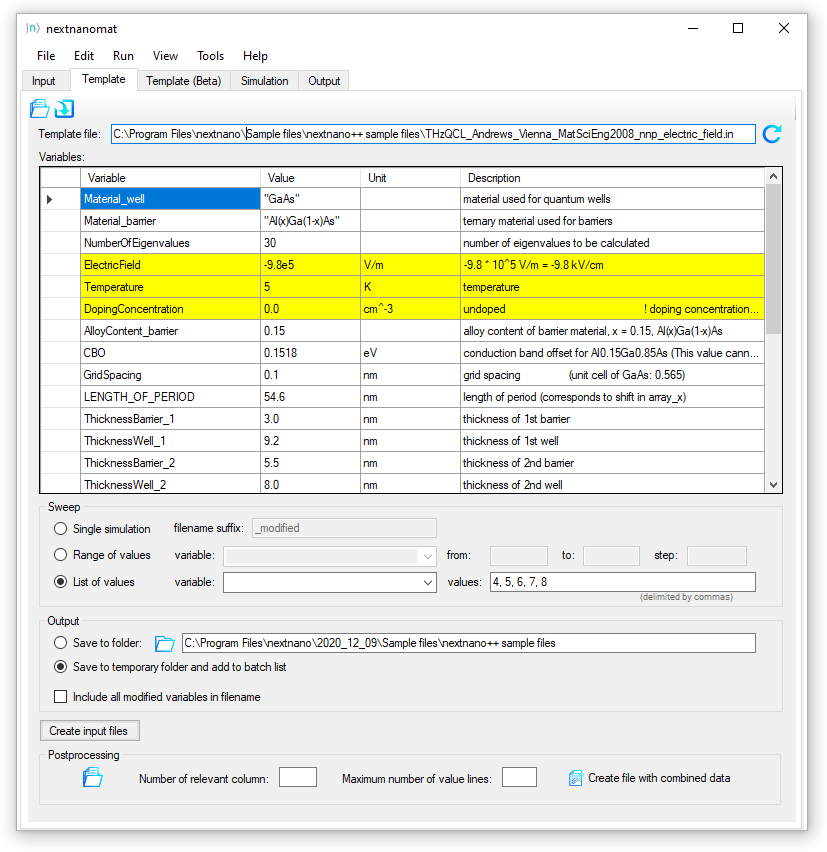
  This input file is parameterized. One can thus use nextnanomat's Template feature to vary e.g. alloy content or barrier widths.
  
  
   
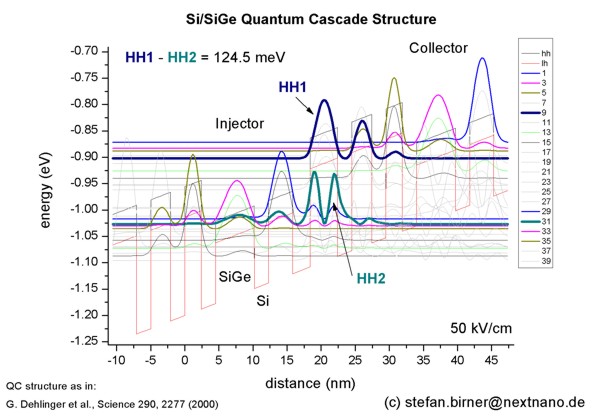
• 9.9 µm, i.e.  30.2 THz or 125 meV (nextnano³ calculation: 124.5 meV)
  Intersubband Electroluminescence from Silicon-Based Quantum Cascade Structures
  G. Dehlinger, L. Diehl, U. Gennser, H. Sigg, J. Faist, K. Ensslin, D. Grützmacher, E. Müller
  Science 290, 2277 (2000)
  
  -> 1DQuantumCascadeLaserSiGe?nn3.in
  
  Note: The Science article reports a calculated transition energy of 130 meV. The experimentally measured value, however, was reported to be 125 meV which is in excellent agreement with the nextnano³ calculations based on the default parameters in the nextnano³ database.
  
  The eigenstates relevant for the optical transitions are the numbers 9 & 10, and 31 & 32.