Approaching large 3D designs with Schrödinger-Poisson self-consistent solver¶
Large memory consumption and long runtimes are usually the challenge when performing 3D-simulations of large devices with high accuracy.
Based in our experience simulating large number of devices, we created a methodology that will assist you to set up the input files in a very efficient way. Figure 2.4.553 summarizes the three phases in the development of these files:
reduction of the dimensionality
optimization of the grid for electrostatics problems
setting up the input file for the quantum computations
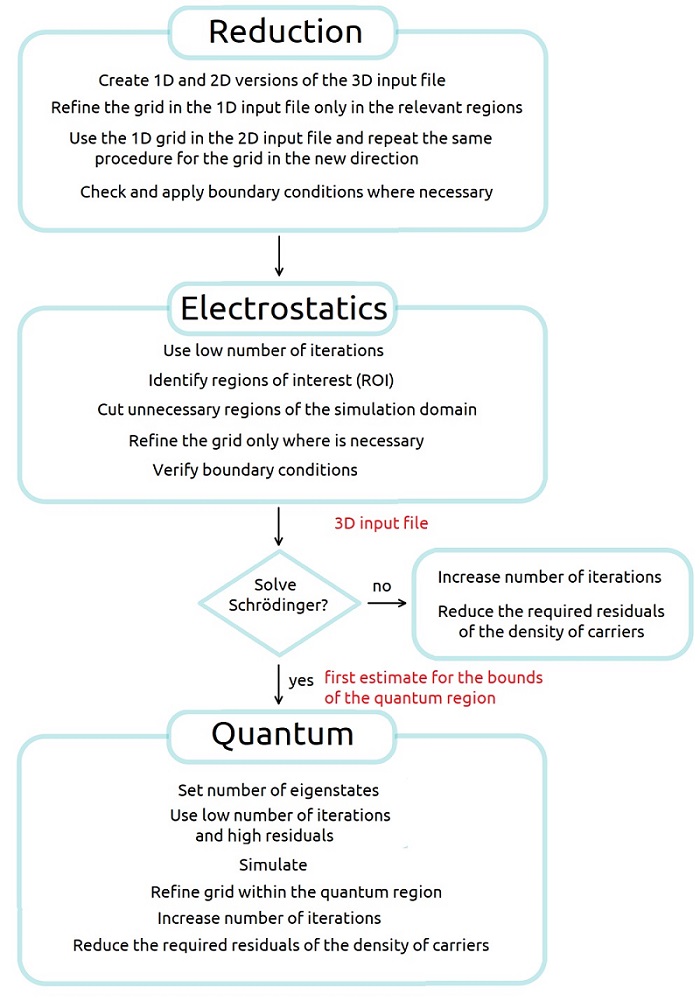
Figure 2.4.553 Methodology for 3D-simulation of large devices.¶
The main idea in all steps is to define the necessary grid in the shorter time as possible. We will focus on the use coarse grids for identifying regions that are more relevant from our simulations.
Reducing the dimensionality of the problem by creating 1D- and 2D- versions of the system are generally very useful to identify which regions do not require a fine grid.
Additionally, by convenient application of boundary conditions, some regions can be completely eliminated from the simulation domain.
A typical example is the substitution of substrate by an adequate boundary condition, that in nextnano++ we denominate contact.
It is important to optimize the grid always step by step: first one dimension, and then, the next.
Even for self-consistent solution of the Schrödinger-Poisson equations we always suggest to set up the input file solving only the Poisson equation, even when not accurate enough. These solutions can be very useful for identifying unnecessary regions to be eliminated from the simulation domain, and to refine the grid only where is actually necessary.
Our focus will be the evolution of the residuals at the beginning of the convergence process. Then, as we mentioned above, it is not expected to obtain accurate results, but only the trends of these residuals.
If no quantum computations are required this would be the point to reduce the residuals in the convergence process for obtaining the results with the accuracy desired.
Similarly, as done in the two previous steps, the definition of the quantum region can be the secret to the final tuning of the 3D-input file. Starting with the results of the electrostatic problem we can identify the regions of interest for such simulations where the grid has to be refined. The identification of a suitable number of eigenvalues for the self-consistent simulations is a crucial procedure that must be performed. It is also important to be aware of the boundary conditions that are adequate at the bounds of the quantum region.
We can take advantage of the one symmetry that the device can present for making a first exploration of these issues. This will save you memory and time.
Each of these procedures are explained in details and with a practical example in three independent tutorials:
where the other guidelines concerning how to simulate large devices in three dimensions efficiently.
Last update: 15/07/2024