— NEW — Optimizing Schrödinger-Poisson self-consistent solver for electrostatic quantum dots

Header

Files for the tutorial located in nextnano++\examples\numerics

• large-3D-systems-schroedinger_3D_nnp_initial.in

• large-3D-systems-schroedinger_3D_nnp_final.in

Scope of the tutorial:

• Guidelines for setting the quantum calculations in 3D-input files of large devices

• Dimensioning the quantum region

Introduced Keywords:

• quantum{ }

• grid{ xgrid{ } ygrid{ } }

Relevant output Files:

• \bias_00000\bandedges_1d_xz_Si_QDs.dat

• \bias_00000\bandedges_1d_yz_Si_QDs.dat

• \bias_00000\iteration_quantum_poisson.dat

• \bias_00000\quantum\probabilities_shift_QuantumRegion_Delta3_1d_xz_Si_2DEG.dat

• \bias_00000\quantum\probabilities_shift_QuantumRegion_Delta3_1d_yz_Si_2DEG.dat

• \bias_00000\quantum\occupation_QuantumRegion_Delta1.dat

• \bias_00000\quantum\occupation_QuantumRegion_Delta2.dat

• \bias_00000\quantum\occupation_QuantumRegion_Delta3.dat

• nn_Large_Devices_3D_initial_version_quantum_nnp.log

Setting up input files for 3D-simulations of the self-consistent Schrödinger-Poisson or self-consistent Schrödinger-current-Poisson system of equations can demand some effort in terms of memory allocation and time consumption, if a systematic approach is missing. This development can become a real challenge when the dimensions of the devices are large (some can be of order of microns) and a fine grid (few nanometers) is required.

This tutorial aims to assist you to reduce such effort, and it is the third part of the methodology Approaching large 3D designs with Schrödinger-Poisson self-consistent solver, that we strongly recommend being followed.

The input file large-3D-systems-schroedinger_3D_nnp_initial.in was obtained in the first two steps of this methodology for the structure that we will very briefly summarize in the next section. This file presents a suitable grid resolution (only sufficient, but not optimally, refined) for obtaining a first estimate of the bounds of the region where the quantum computations will be performed. Unnecessary regions on the devices were eliminated or replaced by convenient boundary conditions.

Following these previous steps are not mandatory for the discussion in the tutorial, but it is very advantageous avoiding grid refinement or performing such tasks directly on 3D-simulations. We remark that there is not a unique way to do it, but it has been used for numerous cases, and provided very good results in most of them.

Device to be simulated

Figure 2.4.571 presents a simplified version of a device that is proposed as a possible semiconductor-based implementation of a quantum computer found in the literature [Kriekouki2022] with dimensions of 400 nm x 800 nm x 70 nm. It consists basically of a 7 nm-Si layer buried in a silicon dioxide layer. By applying bias to the gates deposited at the top of the structure (FTS, FTD, LG1, LG2, and LG3) and at the bottom of the oxide (the back gate) the electrostatic potential can be modified, in order to control the transport of carriers through the silicon layer (the channel of the system). The source and drain are the reservoirs of carriers.

Applying adequate boundary conditions, the simulation domain can be reduced as shown in the Figure 2.4.571 (shown in (b)). The nomenclature of the most important coordinates and sections defined in the input file are summarized in the same image in (c).

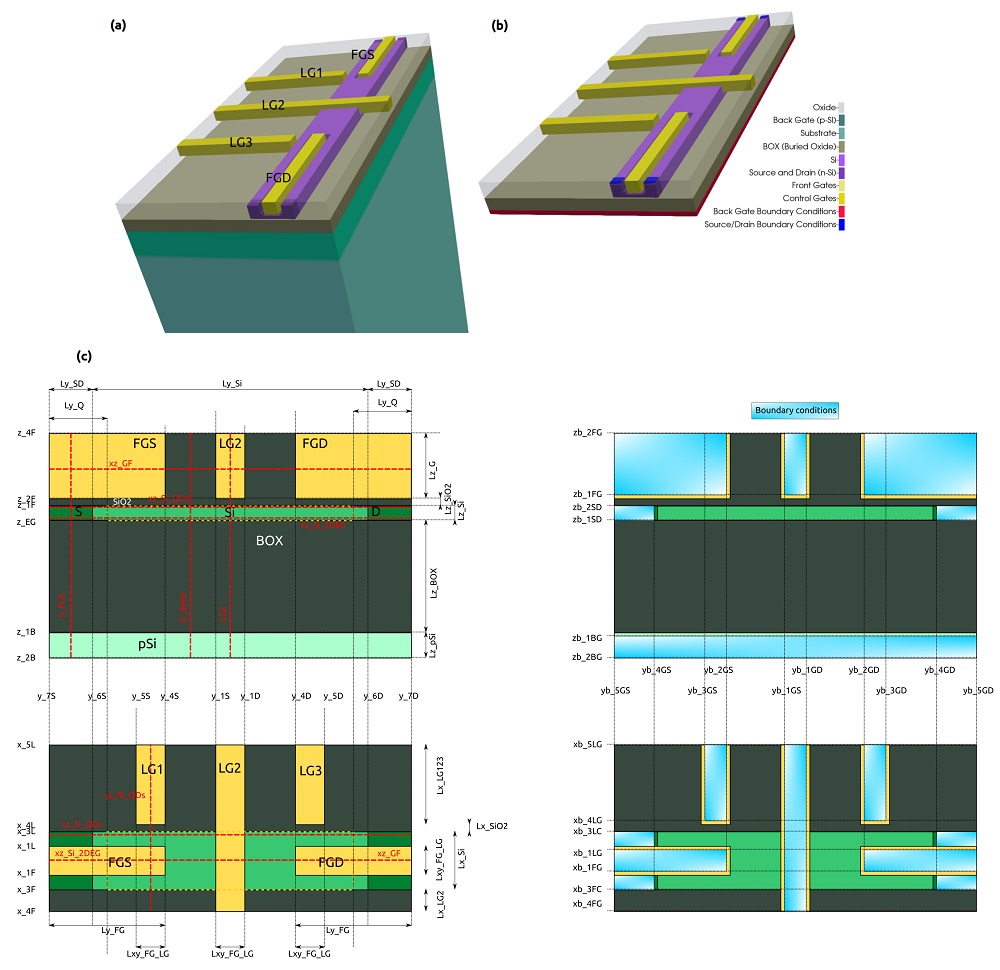
Figure 2.4.571 Device to be simulated. The Si-channel is buried in the oxide. The electrostatic potential is shaped by applying bias to the gates (FTS, FTD, LG1, LG2,LG3 and the back-gate). Source and drain act as reservoirs of carriers propagating through the channel. Device (a) before and (b) after applying adequate boundary conditions. The most important coordinates and sections (dotted lines in red) are shown in (c).

Setting input files for self-consistent calculations of Schrödinger-Poisson equations

As we mentioned before, self-consistent solution of Schrödinger and Poisson equations demands a good strategy in order to reduce the simulation time when tuning the grid. Usually smooth wavefunctions in some region of interest (ROI) require a fine grid resolution and enough number of states to compute the quantum mechanical density of carriers that iteratively will also be used in the solution of the Poisson equation.

Another important issue that show be addressed is the choice of the boundary conditions at the borders of the quantum region. It has to be constantly observed if they are consistent with the models used in the simulation.

Below we present some hints that may be explored for designing an efficient input file for 3D simulations.

Define the goals of the quantum computations

The simulation time of self-consistent Schrödinger-Poisson simulations depends on the time expended in the solution of the Poisson equation and the time for obtaining the quantum solution.

As we showed in previous tutorials, the time for solving the Poisson equation scales with the number of nodes in the grid of the simulation domain. On the other hand, the solution of the Schrödinger equation demands runtimes scaling with the number of nodes in the quantum region, the number of eigenvalues to be computed and also the model and corresponding solver to be used.

Below we will provide some tricks related to these aspects for getting excellent results with less effort.

Optimizing the grid within the quantum regions

1. Defining the bounds of the quantum region: at the beginning does not need to be perfect!

The nodes in the quantum region consist on a subset of the grid points of the simulation domain that are within and at the borders of are region where the Schrödinger equation will be solved. In other words, limiting the size of the quantum region of interest (QROI) and its corresponding grid resolution in the first phase of the quantum simulations will boost the input file development.

Any previous understanding of the physical phenomena in the device may be used to introduce simplifications in the QROI design. Let us present one simplification from our practical example. A quantum dot in the Si channel is expected to be present just in the channel, close to one or both lateral gates (LG1 and LG3) depending on the bias applied to these and the other gates. In this way, if our goal is to compute the density of carriers in the region where the quantum dots appear, the number of nodes of the QROI will represent a very small subset compared with the number of nodes in the whole domain.

A trick for estimating the bounds of the quantum region is to look at the density of electrons from the semi-classical calculations (solving only the Poisson equation). Please, refer to our tutorial — NEW — Optimizing electrostatics simulation for large 3D designs concerning some considerations that may be taken into account. Figure 2.4.572 presents the results of such simulations for the conduction band overlapped with the semi-classical density of electrons for the sections xz_Si_QDs and yz_Si_QDs under a particular combination of biases (0.8V to both front gates, 4 V at LG1 and G3, 1.7 V at the central gate (LG2) and the remaining gates and contacts are grounded). These sections, shown with red dotted lines in Figure 2.4.572, correspond to slices at the region on Si-channel where the quantum dot is expected to be formed.

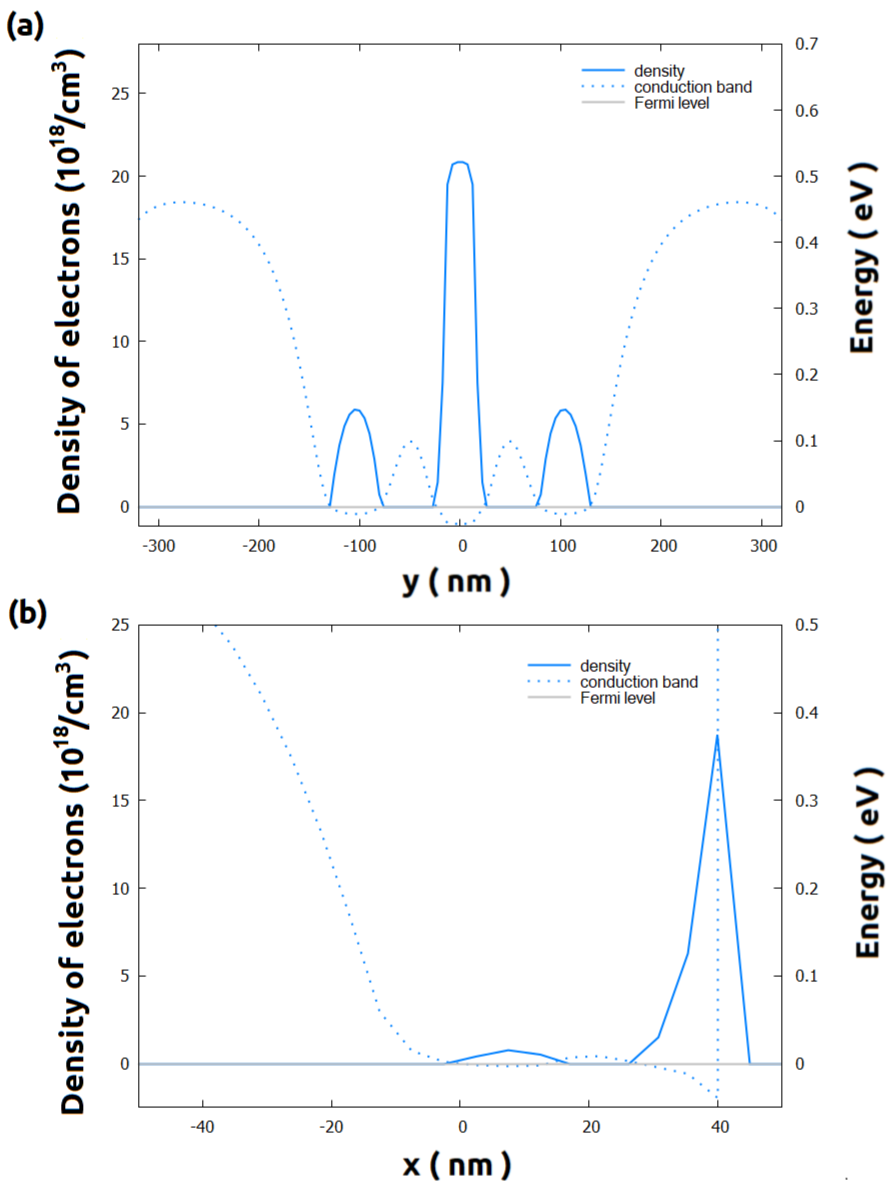
Figure 2.4.572 Conduction band (dotted lines) and semi-classical density of electrons (solid lines) in the slices xz_Si_QDs and yz_Si_QDs (see red dotted lines in Figure 2.4.572), when 0.8 V is applied to both front gates, 4 V to LG1 and LG3 and 1.7 V to the central gate LG2. The remaining gates and contacts are kept grounded.

Although the electrostatic potential is shaped by each specific combination of bias applied to the gates, the bounds of the QROI estimated by the semi-classical electron distribution does not change too much if the biases are around the first operation point, as we showed in the tutorial concerning the electrostatic calculations mentioned above. The bounds of the QROI resulting from this analysis are x = [-40, 40], y = [-150, 150] and z = [0, 7].

The device of our example presents a geometrical symmetry related to the plane y = 0. We can take advantage of this property by reducing even more the QROI for the first tuning of the parameters concerning quantum computations. Our main objective here is not even to get good results, but to have a first idea about the convergence process of the system of equations, the required grid resolution within the quantum region, and to verify if the boundary conditions at the borders are satisfied.

In this way we can weak a little the criteria of the convergence of the quantum_poisson solver, requiring a low number of iterations (for example 10 iterations, or $quantum_iterations = 10). Keeping these requirements in mind we can start defining a reduced QROI with y = -150 and y= -50 as the bounds in the y-direction.

Hint

You can save some time and storage disabling all outputs files that are not relevant or did not change from one run to the other, like contacts, intrinsic density, and material.

2. Finding a suitable number of eigenvalues

The Hamiltonian to be solved in the Schrödinger equation is specified in the section quantum{ } of the input file. In the section quantum{ region{ } } of our documentation you will find the models currently implemented in nextnano++. Independent of your choice we recommend to use at this point the computationally lighter one: the single-band. The relevant bands to be taken into account in these calculations must be defined in the input file. In our example, the band gap of silicon, the material of the region of interest, is defined by the minimum of the Delta band.

As we mentioned above, we need to choose a number of eigenvalues enough to compute the density of carriers from the wavefunctions obtained after each quantum iteration. This quantity will be injected in the Poisson equation in the next iteration, and a new electrostatic potential will be computed. Then, here we need to do a trade-off: the number of states can not be too small, but also not too large.

Low number of computed states generates truncated quantum density that, when included in the next iteration of the solver of Poisson equation, may change the electrostatic potential in another direction, and more frequently may not converge. On other hand larger number of states will require more computational effort unnecessary for this first tuning.

How to choose a suitable number of eigenvalues? The answer is simple: guess, compare and improve. Remember: our grid is still coarse. Then, this is the best moment to explore a first guess. We recommend that, starting with 10 states, for example, to increase this number and compare some relevant results iteratively, instead of simply sweeping the variable $N_states in our input file.

Now it is time to perform the first calculations. Remember: what it is important to observe here is how the residuals behave during the convergence process when new states are added. Figure 2.4.573 shows the evolution of the residual of the density of electrons as function of the number of eigenvalues. We can see that the residual decay faster when more states are included in the computation. The resulting conduction band in two relevant sections does not change substantially for number of states larger than 20. The reason for this can be inferred from the occupation number for one of the Delta bands: it is required computing at least 20 states in order to converge that 4 states are actually occupied.

Figure 2.4.573 Results of the self-consistent Schrödinger-Poisson simulations, in the reduced QROI as function of the number of eigenstates computed, after 10 iterations. (a) The evolution of the residuals, (b) and (c) the conduction band for the sections xz_Si_QDs and yz_Si_QDs, respectively, and (d) the occupation number after only 10 iterations. These are intermediate results: the convergence process was still not completed.

Please, be aware: we still are not getting the solutions of the system (look at the log files in the output folder, large-3D-systems-schroedinger_3D_nnp_initial.log). The system is still coarse, and probably we are still very far from the minimum residuals to be reached, for stopping the process. Nevertheless, this behavior of the residuals tells us that we are in the right direction.

3. Making the grid fine in the quantum region

Let us take a look at the wavefunctions in the computations using 20 eigenstates ($N_states = 20) shown in Figure 2.4.574 for the same sections of Figure 2.4.573. It is more convenient to use the results of the output file \bias_00000\quantum\probabilities_shift_QuantumRegion_Delta3_1d_xz_Si_2DEG.dat or \bias_00000\quantum\probabilities_shift_QuantumRegion_Delta3_1d_xz_Si_2DEG.dat that represent the values of the density probabilities in a section, shifted by the correspondent eigenvalue. From this reason, from this point to the end of this tutorial “wavefunction” actually means shifted probability density. The first observation is that the boundary conditions for the quantum conditions looks being suitable for the band edges in this region. Nevertheless, the grid resolution in the x- and y-directions is actually too coarse, as expected.

Figure 2.4.574 Wavefunctions overlapped to the conduction band from self-consistent quantum-Poisson simulations for the sections (a) xz_Si_QDs and (b) yz_Si_QDs. The “quantum” density of electrons were computed considering 20 states and a grid resolution of 5 nm in the y-direction. These are intermediate results: the convergence process was stopped after 10 iterations.

To avoid explosion of the number of nodes to be simulated, we suggest modifying the grid definition by introducing new variables for the control of the grid space only within the quantum region. Including the bounds of the quantum region in the grid is also highly recommended. In our example, our previous definition of the grid in x- and y-direction:

    xgrid{
        line{ pos = $x_4F spacing = $space_x_4F }
        line{ pos = $x_3F spacing = $space_x_Si }
        line{ pos = $x_1F spacing = $space_x_Si }

        line{ pos = $x_1L spacing = $space_x_Si }
        line{ pos = $x_3L spacing = $space_x_Si }
        line{ pos = $x_4L spacing = $space_x_4L }
        line{ pos = $x_5L spacing = $space_x_5L }
    }

    ygrid{
        line{ pos = $y_7S spacing = $space_y_SD }
        line{ pos = $y_6S spacing = $space_y_SD }
        line{ pos = $y_5S spacing = $space_y_LG }
        line{ pos = $y_4S spacing = $space_y_LG }
        line{ pos = $y_1S spacing = $space_y_LG }
        line{ pos = $y_1D spacing = $space_y_LG }
        line{ pos = $y_4D spacing = $space_y_LG }
        line{ pos = $y_5D spacing = $space_y_LG }
        line{ pos = $y_6D spacing = $space_y_SD }
        line{ pos = $y_7D spacing = $space_y_SD }
    }

will be changed to

    xgrid{
        line{ pos = $x_4F spacing = $space_x_4F }
        line{ pos = $x_3F spacing = $space_x_Si }           # bound of the quantum region
        line{ pos = $x_1F spacing = $space_x_QR }

        line{ pos = $x_1L spacing = $space_x_QR }
        line{ pos = $x_3L spacing = $space_x_QR }           # bound of the quantum region
        line{ pos = $x_4L spacing = $space_x_4L }
        line{ pos = $x_5L spacing = $space_x_5L }
    }

    ygrid{
        line{ pos = $y_7S spacing = $space_y_SD }
        line{ pos = $y_6S spacing = $space_y_SD }

        line{ pos = $yq_min spacing = $space_y_QR }           # bound of the quantum region
        line{ pos = $y_5S   spacing = $space_y_QR }
        line{ pos = $y_4S   spacing = $space_y_QR }
        line{ pos = $y_1S   spacing = $space_y_QR }
        line{ pos = $y_1D   spacing = $space_y_QR }
        line{ pos = $y_4D   spacing = $space_y_QR }
        line{ pos = $y_5D   spacing = $space_y_QR }
        line{ pos = $yq_max spacing = $space_y_QR }           # bound of the quantum region

        line{ pos = $y_6D spacing = $space_y_SD }
        line{ pos = $y_7D spacing = $space_y_SD }
    }

where $space_x_QR and $space_y_QR will control the grid resolution within the quantum region, and $yq_min and $yq_max are the bounds of this region in the y-direction.

Instead of refining both axes at the same time, let us reduce the grid resolution in the y-direction first. Figure 2.4.575 presents the wavefunctions overlapped with the band edges in the section xz_Si_QDs for different grid spacing in the y-direction controlled by $space_y_QR. We can also observe the corresponding residual evolution in the first 10 iterations. The grid in the x-direction was kept 5 nm.

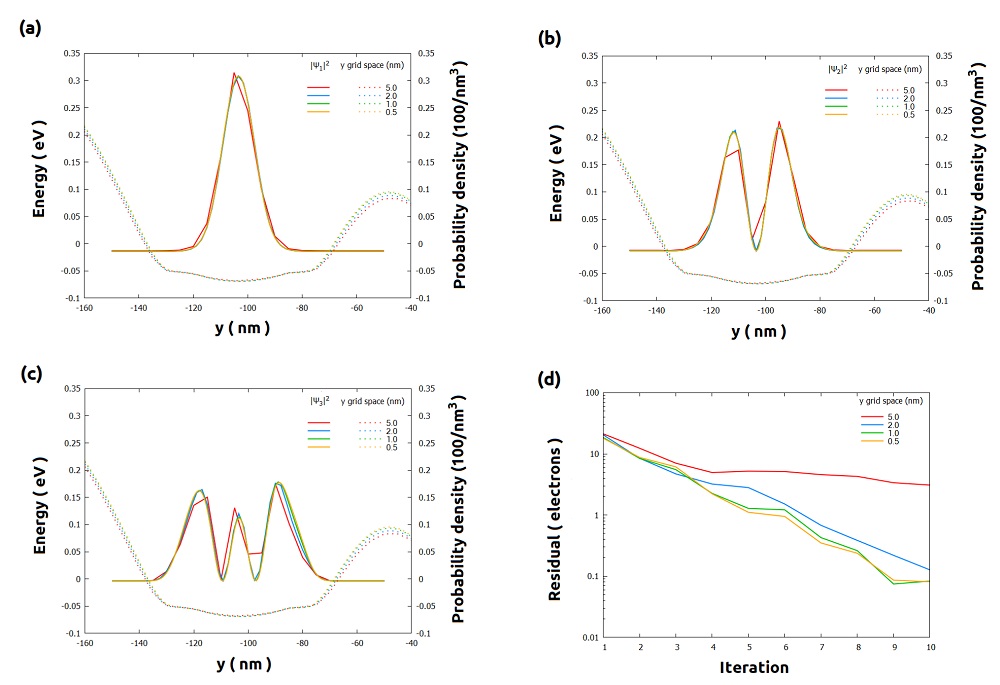
Figure 2.4.575 Results of the self-consistent Schrödinger-Poisson simulations using different grid spacing in the y-direction only within the reduced QROI (section xz_Si_QDs). (a) -(c) wavefunctions (solid lines) for the three lowest states overlapped with the conduction band (dotted lines) (d) residual evolution. These are intermediate results after only 10 iterations: the convergence process was still not completed.

The evolution of the residuals are very similar, except for the case of 5 nm. Additionally, for $space_y_QR of 1 nm or less the wavefunctions are smooth and do not present relevant changes.

Repeating a similar procedure for different grid resolutions in the x-direction ($space_x_QR) we obtain the wavefunctions of the Figure 2.4.576. In the y-direction the grid resolution in this region was considered equal to 1 nm ($space_y_QR = 1 in our input file).

Figure 2.4.576 Results of the self-consistent Schrödinger-Poisson simulations for section yz_Si_QDs using different grid spacing in the x-direction within the QROI: (a)-(d) wavefunctions (solid lines) for the four lowest states overlapped with the conduction band (dotted lines), and (e) residual evolution. These are intermediate results after only 10 iterations: the convergence process was still not completed. $space_y_QR was kept 5 nm.

From analysis of these plots, we observe that decreasing the grid resolution in the x-direction from 1 nm to 0.5 nm does not introduce significant improvement in the computation of the density of probabilities from the wavefunctions in the first 10 iterations. For this reason, we infer that values of 1 nm or less for $space_x_QR and $space_y_QR will be required for more accurate simulations.

4. Expanding the Quantum Region: time to get beautiful plots (and accurate results)!

Using the results obtained for reduced QROI, we can now design the whole quantum region, now extended from -150 nm to 150 nm for the y-direction. Until now the central valley of the conduction band in Figure 2.4.572 (around y = 0) was not part of the reduced QROI. Therefore, it may require to increase the number of the eigenvalues in the self-consistent computations in order to fill also this region with carriers.

How to estimate the minimum number of eigenvalues required ($Nstates)?

Our hint is to use, once again, our lower resolution grid within the quantum region (for example, with 5 nm) and few iterations (10) for this tuning. We will reserve the finer grid (1 nm) we previously obtained, only to get the final accurate results. Figure 2.4.577 illustrates a sequence of simulations where the grid resolution and the number of states were iteratively changed.

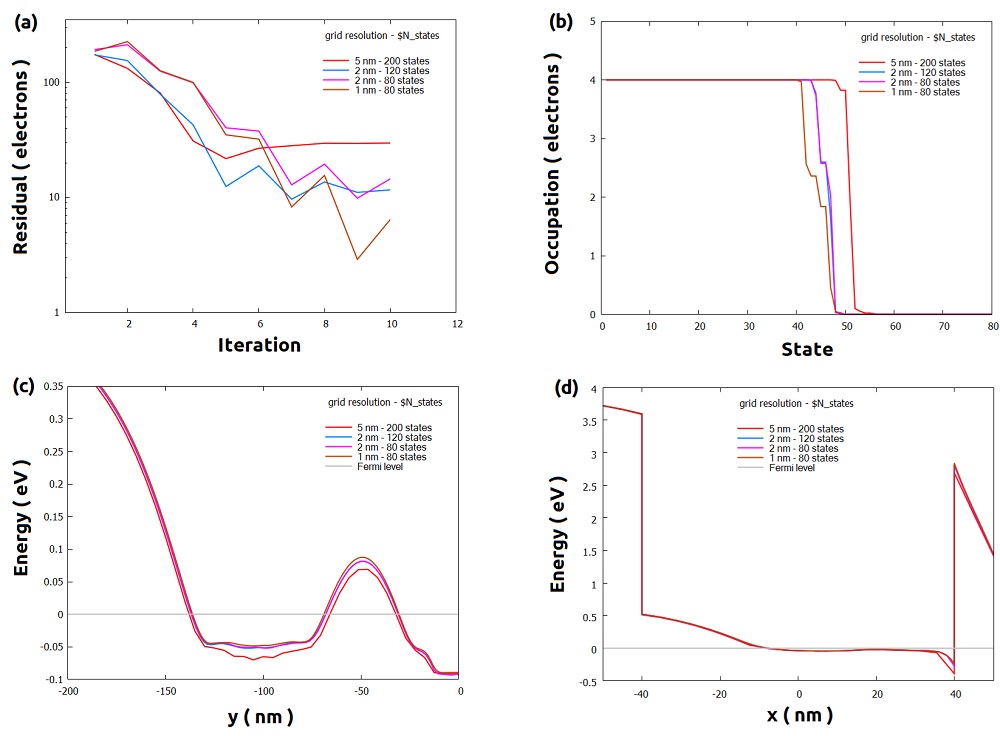
Figure 2.4.577 Sequence of simulations for defining a suitable value for $Nstates. (a) residual evolution, (b) occupation number of the most populated band, (c) and (d) conduction band for the sections xz_Si_QDs and yz_Si_QDs, respectively. These are intermediate results (only 10 iterations of the coupled solvers were taken into account).

From the coarser grid we observed that the occupation number in the most populated band it is no more than 80 states. The residual of the density of electrons decreases as the grid gets finer and the number of states is around 80. The conduction band in the more relevant sections, shown in the image, does not change too much, for grid spacing less than 2 nm in the quantum region.

Now it is time to obtain more accurate results. As we mentioned before we will compute 80 states in a quantum grid with $space_x_QR = 1 and $space_y_QR = 1. The convergence process will be controlled by the maximum number of iterations ($quantum_iterations = 100) and the accuracy desired ($CRes) for the residual of the quantum densities. The solutions converge when the quantum density of electrons is smaller than $Cres before ending the total number of iterations of the self-consistent calculations.

We start, for example, with a constraint $CRes = 1 and, gradually we decrease until the solutions do not change.

Figure 2.4.578 shows an example how to choose a suitable value for $CRes. This corresponds to simulations that converged in less than 100 iterations. The curves correspond to some wavefunctions for the section xz_Si_QDs when requesting accuracy of 0.1, 0.01 and 1.0. We observe that the lowest states (like shown in (a)) are more requires more deep constraints in the value of $CRes than the highest states. Nevertheless, decreasing this parameter from 0.10 to 0.01 does not present a significant improvement in the results. What you need to keep in mind is which of both values to use: using $CRes = 0.01 will produce, in thesis, better results, but it will result in longer runtimes and more memory for storing the results.

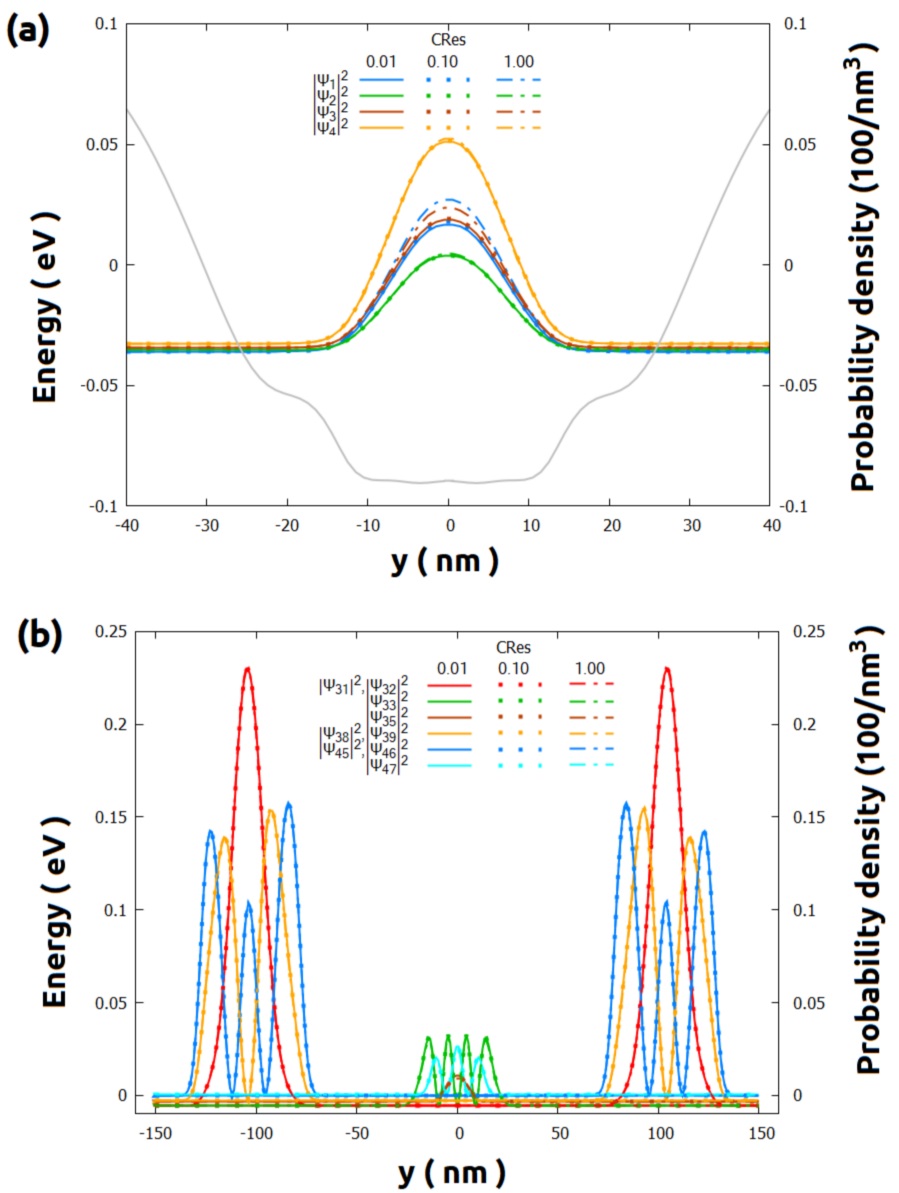
Figure 2.4.578 Some wavefunctions in the section xz_Si_QDs as function of the residual used in the convergence process $CRes. (a) in the central, and (b) in the whole quantum region. All solutions converged before reaching the maximum number of iterations (100).

The solutions for the section yz_Si_QDs are even more robust than the previous one (see Figure 2.4.579): the wavefunctions do not present relevant variation even when the value of $Cres is higher.

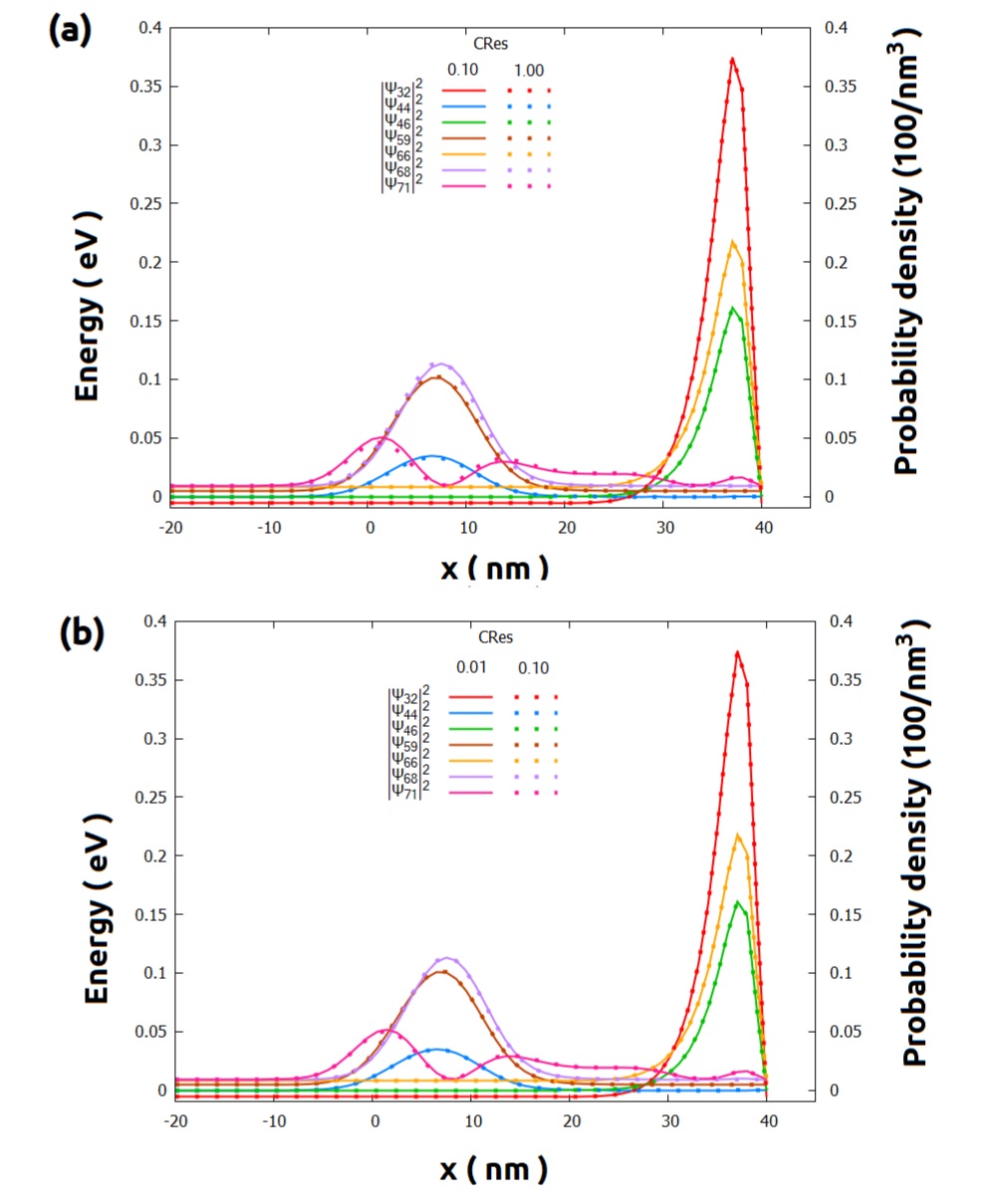
Figure 2.4.579 Comparison of some wavefunctions in the section yz_Si_QDs for convergence residual ($Cres) (a) from 1.00 to 0.10, and (b) from 0.10 to 0.01. All solutions converged before reaching the maximum number of iterations (100).

Hint

Requiring higher accuracy of the solutions may result in large runtime, when the decrease of residuals are too slow, or even the process does not converge within the chosen maximum number of iterations. Therefore, it is a good practice tracking the residual evolution during the simulations. If they are taking too long (compared with another previous one) for decreasing, you always can interrupt the calculations pressing the key F11 or F12.

Final considerations

Last but not least, we will simply mention here some important topics are worth to be discussed in separated tutorials.

For some problems that requires really fine grids in very large regions the memory may become the bottleneck of the simulations: the system to be solved may not fit in your RAM. For these situations we implemented in nextnano++ the decomposition method, that converts the 3D-Schrödinger-Poisson problem in multiples 1D problems. Additionally, our implementation results very fast. Nevertheless, this algorithm has intrinsic assumptions, that may not apply to all devices and shall be carefully used. For more detail look at in our page quantum{ region{ quantize…{ } } } of our documentation.

Nevertheless, this algorithm has intrinsic assumptions, that may not apply to all devices and shall be carefully used.

It is also important to mention that, coherent quantum transport calculations can be performed using the nextnano++ implementation of the CBR method. The performance of these computations can be improved implementing small changes in the final input file from this tutorial. The most important modification consists on importing the file with the final result of the electrostatic potential from your self-consistent simulations, instead of being solved directly. Our tutorial Landauer conductance and conductance quantization: from quantum wires to quantum point contacts presents this method in detail and the corresponding input files than can be easily extended to 3D devices.

One again, we remind you that in this tutorial we considered only a combination of biases applied to the gates. It is always convenient to check the constraints (boundary conditions for the quantum region, occupation number, residual evolution, etc.) to another scenarios.

We recommend visiting our documentation, where we present the whole methodology Approaching large 3D designs with Schrödinger-Poisson self-consistent solver and its first two steps:

— NEW — Reducing dimensionality of large 3D designs

— NEW — Optimizing electrostatics simulation for large 3D designs

Last update: 15/07/2024